Comparisons: Borda Count 2
Teaming and the Borda Count
Despite its many good properties, the Borda Count is highly and stubbornly vulnerable to teaming. Even Borda himself recognised this problem and declared that his system was for "honest men" only. To appreciate its inability to combat teaming, the previous three tables (see the Evaluations: Clones & Teaming 5 page) for a single-winner two-candidate election and tied outcome are repeated below but with the Borda Count replacing CHPV as the voting system.

With half of the voters supporting candidate A and the other half voting for B, a two-way critical tie initially results. Party A then nominates two clones A1 and A2 in place of A to try to gain unfair advantage. With no slate issued, these clones are identical and the tie is retained; see table opposite. Note that, unlike for CHPV and FPTP, there is no vote splitting here so no self-harm occurs. In fact, the previous single tally for A has not been halved (as in FPTP) but duplicated instead.
Once a slate is issued and adhered to by A supporters, the two clones are converted into fraternal ones and the desired teaming is then generated. A forward slate ensures that A1 beats B (as shown in the table below left) while a reverse slate ensures that A2 beats B instead. If B retaliates with the standard tit-for-tat reversal of whichever slate A issued, only then is the tie between the two parties restored; see table below right. Note however that it is now a three-way tie due to the duplication of the tally for A.


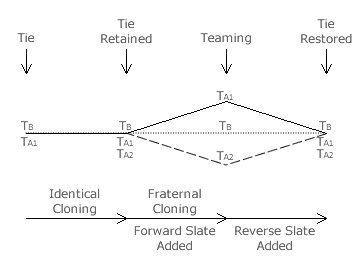
The figure opposite illustrates the effects of the introduction of the identical clones, converting them into fraternal clones using a forward slate and then combating this with a reverse slate. Notice that the tally for B is unchanged throughout as the voter preferences for or against B are unaltered. Further notice that the combined tally for both clones is also unchanged and that crucially it is twice that of the tally for B. Hence, when the two clones have different tallies, one will beat B while the other will lose to B. Unless there is a tie, B always comes second and loses to either A1 or A2. Even when tied, B loses out since A has two chances of being selected at random as the winner while B has only the one.
Party A has everything to gain and nothing to lose by teaming. For the Borda Count, the strategy of slate reversal simply does not work and party B is forced to respond by adding its own slate of two clones. Party A could then add a third clone with party B responding likewise. The nightmare scenario then beckons where the party that can nominate the most clones gains the greater (unfair) advantage. Teaming is indeed an inherent and intractable problem for the Borda Count.
A comparison of the effects of teaming in Borda Count and in CHPV elections will be addressed in detail in the upcoming Comparisons: Geometric Voting section. Before preceding here, the relationship between the Borda Count and GV with a common ratio approaching one must be addressed.
Proceed to next page > Comparisons: Borda Count 3
Return to previous page > Comparisons: Borda Count 1
