Comparisons: D'Hondt ~ Party Cloning 2

Comparative Susceptibility of CHPV and the D'Hondt Method to Party Cloning

The party cloning threshold figures for CHPV are presented in the earlier Evaluations: Party Cloning section. To enable a direct comparison between the susceptibility of CHPV and the D'Hondt method to party cloning, the relevant threshold figures for up to six winners are repeated below left for D'Hondt and below right for CHPV.

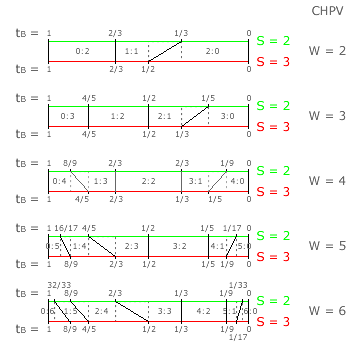
Where elections are held here with two or three winners (W), CHPV is not susceptible to party cloning. For four, five or six winners, CHPV is only vulnerable when party B already has the majority share of the vote. With a minority share, party B gains nothing at best but risks harming itself quite significantly.

As the D'Hondt method is never vulnerable to party cloning in this election scenario, CHPV cannot outperform it in this respect. However, as shown in the previous section, CHPV does have a significantly higher optimality than the D'Hondt method when its optimality is around its peak value. This peak varies with the number of parties competing in a CHPV election but it occurs at about four or five seats for up to nine parties.

As party-list CHPV elections are conducted concurrently across multiple few-winner constituencies, outcomes are significantly more likely to be optimally proportional than those where the D'Hondt approach is used instead. However, it is critical with CHPV to ensure that the number of seats per constituency is optimal for the anticipated number of parties that will contest an election. Otherwise, the D'Hondt method is likely to produce the more proportional set of results.

Proceed to next section > Comparisons: D'Hondt ~ Proportionality

Return to previous page > Comparisons: D'Hondt ~ Party Cloning 1