Comparisons: Sainte-Laguë ~ Optimality 2

Comparative Optimality in Two- and Three-Party CHPV and Sainte-Laguë Party-List Elections

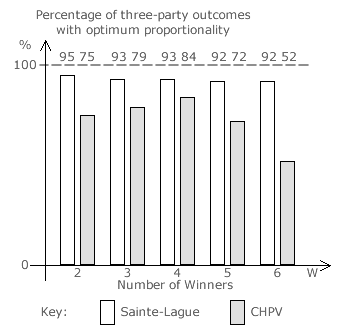
In the earlier Evaluations: Optimality of CHPV section, the proportion of CHPV outcomes with optimum proportionality in two-party and three-party elections is already established. These results can now be compared directly with those for Sainte-Laguë optimality; see previous page. The bar chart below left presents a comparison between Sainte-Laguë and CHPV for two-party elections and the one below right is for three-party elections.

For two-party contests, the Sainte-Laguë method always generates an optimally proportional outcome. Clearly, CHPV does not achieve 100% optimality for any given number of winners.

For three-party contests, Sainte-Laguë optimality is very high with just two winners but it is not perfect. As extra seats are added, this initial optimality declines very slowly while for CHPV it drops quickly after initially rising up from 75%. Here the optimality of CHPV even at its peak (84% at W = 4) never exceeds the level achieved by the Sainte-Laguë method.

In terms of optimality, the Sainte-Laguë method always outperforms CHPV regardless of the number of winners or parties in the party-list election.

Proceed to next section > Comparisons: Sainte-Laguë ~ Party Cloning

Return to previous page > Comparisons: Sainte-Laguë ~ Optimality 1