Evaluations: CHPV Maps 3
Three-Party Multiple-Winner CHPV Elections (continued)
Consider what happens when extra winners are increasingly added. For the OPV domains, they get smaller in size but they remain as regular hexagons of equal area (albeit that peripheral ones are truncated) and are still evenly distributed across the map. However, for the CHPV domains, they differ is shape and area as extra winners are added. Domains shrink in size depending upon how close they are to the centre of the triangular map. Those near the centre are the largest and those furthest away are the smallest.
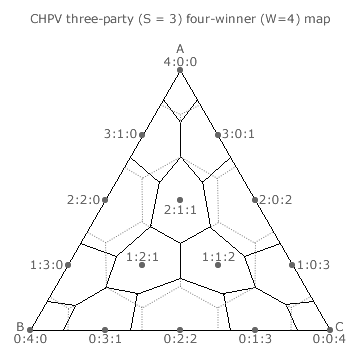
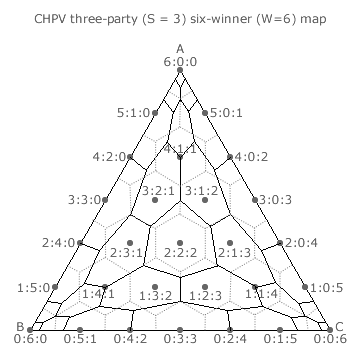
The large central domain for three, six, nine and other integer multiples of three winners is the same size and shape on each map. However, the domains in the three corners rapidly become tiny as further winners are included. It is therefore clear that when large numbers of winners are required from three-party contests an increasing number of outcomes are not optimally proportional.
Indeed, even perfect proportionality between party tally share and party seat share may not be achievable when there are a large number of winners. Consider the case where there are six winners (W = 6) and the tally share is exactly 5:1:0. The ideal seat share is clearly also 5:1:0. However, the 5:1:0 dot on the map is in the 4:2:0 CHPV domain and the outcome is hence neither perfect nor optimal.
For less than five winners, all dots are within their appropriate CHPV domains. For five winners, six dots (4:1:0, 1:4:0, 4:0:1, 1:0:4, 0:4:1 and 0:1:4) coincide with a CHPV domain boundary and a perfect outcome is dependent on a random tie-break. Increasingly, for more than five winners, some dots appear in an inappropriate CHPV domain.
This threshold of five winners is the same as that for the two-party maps. This is to be expected since each edge of the map is equivalent to a two-party map; as along each edge one party has a zero share of the vote.

Proceed to next section > Evaluations: Optimality
Return to previous page > Evaluations: CHPV Maps 2
