Evaluations: Proportionality of CHPV 2

Disproportionality due to Voting System

Any voting system other than an OPV one will also have discrepancies due to seat resolution. However, the number of domains will be a constant for a given number of winners (W) and parties (S) regardless of the particular voting system employed. This means that the average size of a domain will also be fixed and hence independent of the actual voting system. For OPV, the worst case LSI_RES applies to each and every domain as they are all identical regular hexagons (before any truncation by a map edge). Therefore, for any other system, the resolution LSI for a particular election outcome will vary (as domain shapes and sizes vary) but on average it will be very similar to the 'benchmark' OPV one (as the number of domains is constant). On this basis, disproportionality due to seat resolution and disproportionality introduced by the voting system itself can be disentangled and measured separately using two indices; one for each.

As can be seen from the earlier two- and three-party maps, the CHPV domains and their boundaries are displaced relative to the OPV ones. The worst case LSI_RES is a measure of the difference between the centre of an OPV domain where perfect proportionality is achieved (LSI = 0) and any corner extremity of the full hexagonal domain where all parties tie for the last seat. For the voting system LSI, it is hence reasonable to use instead the displacement of the centre of an actual CHPV (or other) domain relative to its perfect OPV domain centre. As this difference between the two corresponding centres grows, so the centre offset least squares index (LSI_j) for domain j increases; indicating worsening disproportionality.

The voting system LSI must include all the LSI_j domain indices rather than just an arbitrary one. The formula opposite defines this voting system LSI in terms of all its domain centre offset indices. As the individual domain indices range from 0 to 1, then dividing by the total number of domains (k) within the square root ensures that the LSI_VS also ranges from 0 to 1. The resultant LSI_VS for any given S-party W-winner party-list CHPV election can then be compared directly to that of an equivalent election that uses another voting system; see Comparisons chapter.

It is important to note that the LSI_VS for OPV is by definition zero. The only disproportionality present in OPV is that due to seat resolution (LSI_RES) alone. Hence, OPV is not a perfect party-proportional voting system but simply an optimal one.

CHPV Domain Centres

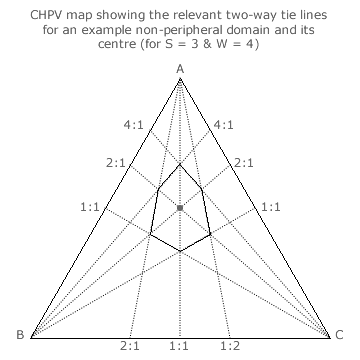
In order to determine the LSI_VS for any particular multiple-party multiple-winner CHPV election, the position of each domain centre must first be identified. In the example three-party map opposite, one of the non-peripheral domains for a four-winner election is illustrated.

Three two-way tie lines are drawn as dotted lines from each apex. For example, from apex C the 4:1, 2:1 and 1:1 tie lines for parties A:B are shown. The relevant critical section (shown as full lines) of the 4:1 and 1:1 tie lines form two opposing sides of the irregular hexagonal domain. A section of the intervening non-critical 2:1 tie line forms a diagonal between two opposing corners (three-way ties) of the domain. Similarly, for each apex, sections of the two outer tie lines form the domain boundary and a section of the intervening tie line forms a central diagonal.

Notice that the three intervening non-critical two-way tie lines necessarily intersect at the same point and that this point is hence a non-critical three-way tie. Within the domain, the tie lines form the three central diagonals of the irregular hexagon. The central three-way tie point is therefore defined as the centre of the domain.

For the example domain shown, its centre is where parties A:B:C have tallies in the ratio of 2:1:1. By this method, the centre point of every non-peripheral domain within the triangular three-party map can be established.

For a domain truncated by at least one map edge, the method of determining its centre as the intersection of three diagonals is essentially the same. For two-party maps, it is again a non-critical intervening tie between the two domain ends (critical ties) that defines each domain centre here. For more than three parties, a tabular approach has to be adopted in place of the visual maps. It employs a simple formula for deriving the domain centre tally shares from the domain seat shares. There is one formula for peripheral domains and another for non-peripheral ones. For more details on finding the centre of any CHPV domain, please refer to proof EP2 on the next page.

Proceed to next page > Evaluations: Proportionality 3

Return to previous page > Evaluations: Proportionality 1