Comparisons: Geometric Voting 10

Comparison of Voting System Susceptibilities (continued)

The truncated map opposite is the left-hand corner of the three-candidate map where candidate A either wins or ties. All such election outcomes are located in the six coloured sectors of the map. A voting system with weightings 1-x, x and 0 is depicted here. As T_A = 1-x is the maximum per-unit tally that A can achieve, there are no outcomes between this threshold and apex A.

• For a full explanation:
  Refer to proof CG8

As described earlier, if tactical voters bury A in favour of B the sincere election outcome is shifted parallel to the AC baseline towards or into the ranking region where B scores a tactical win. This is illustrated by the 'B wins as A buried' arrow on the map. Similarly, the 'C wins as A buried' arrow illustrates how C may win instead of B. The tactical option of burying is only potentially effective in sectors 2 and 3 for B and in sectors 5 and 6 for C given the directional constraints on the map of any shift. If the magnitude of this shift is too small, the burying tactic will fail. If excessively large, the least preferred candidate may inadvertently win.

The lifting tactic is only potentially effective in sectors 3, 4 and 5 for either B or C to win. The 'B lifted to beat A' and the 'C lifted to beat A' arrows illustrate these tactical options and the directional constraints on any shift here. Note that the shift for B is in direct opposition to that for C. The net magnitude of any shift will determine whether this tactic succeeds in dislodging A or not. In sector 1, there is no potential for successful tactical voting of either type. If a tactical voter does bury A here, their least preferred candidate leapfrogs into first place instead! Also in sector 1, it is impossible to score a tactical win through lifting.

For each of the four positional voting systems, all their outcomes can be derived from the 1035 election profiles. These outcomes may then be plotted on a three-candidate map specific to the voting system. Where an outcome falls within a given map sector determines whether any tactical option might be available for this particular election profile. Even if the outcome is in the relevant sector, the tactic may still not be available for some of the election profiles that generate it. For a tactical win for B to occur by casting B>C>A, burying A requires an initial sincere B>A>C ballot to exist and lifting B needs an initial sincere C>B>A ballot to exist. If neither exists, neither tactical option exists despite the outcome being in the relevant sector. The table below defines the number of tactical options available to a sole tactical B supporter given this election and the voting system.

• For full details of the election maps, outcomes, profiles, tactical options and other data:
  Refer to proof CG8

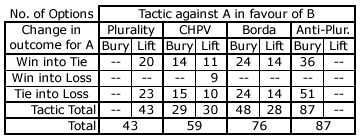
For plurality, burying is not an option as swapping the two worthless lower preferences over has no affect. Similarly for anti-plurality, lifting is not an option as swapping the two equal-value higher preferences is pointless. As can be seen on the above map, sector 1 recedes in area as the weighting x increases and the T_A = 1-x threshold retreats away from apex A. Indeed, sectors 2 and 6 also recede as x rises above 1/3 and all three sectors vanish for anti-plurality where x = 1/2. So, as x steadily increases, ever more election profiles produce outcomes that occur closer to the critically-tied ranking region boundaries where a single tactical voter may engineer a tactical gain. Further, when x < 1/3 the magnitude of any shift is greater for a lifted outcome than for a buried one. For x > 1/3, the reverse is true.

If the sincere election outcome is a critical tie, a sole voter may then score a tactical win for B over A. This voter may also be able to generate a tactical tie if the sincere outcome is sufficiently adjacent to this tie. For B, a win is better than a tie and a tie is better than a loss so either is a tactical gain. For the Borda Count where x = 1/3, the bury and lift magnitudes are equal and hence a sincere win may be converted into a critical tie but never into a loss with just a single tactical ballot. Where the magnitudes differ, the larger shift may however convert a win into a loss with only one (bury or lift) tactical ballot.

In conclusion, burying is increasingly effective as x increases while lifting is increasingly productive as x decreases. A Borda Count election is more prone to burying than a CHPV one as burying shifts are larger and more election profiles generate outcomes that are in the vicinity of critical ties. However, a CHPV election is more prone to lifting than a Borda Count one as the magnitude of such shifts is greater here. Plurality is highly vulnerable to compromise lifting while anti-plurality is similarly very susceptible to burying. For these two strictly non-positional voting systems, tactical voting only requires a perception of how other voters may cast their one and only true option of voting for or against a particular candidate. For genuine positional voting systems, tactical voters need a perception of how all the preferences of other voters might be cast so consequently fewer attempts at tactical voting are likely to be made or to prove successful.

Proceed to next page > Comparisons: Geometric Voting 11

Return to previous page > Comparisons: Geometric Voting 9