Comparisons: Geometric Voting 2

Identifying Equivalent Three-Candidate Voting Systems

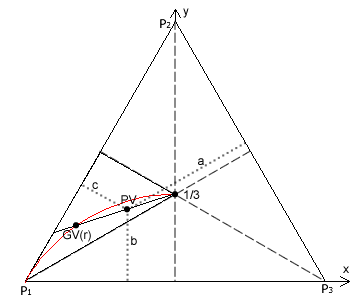
The preference map for a three-candidate positional voting system displayed on page 1 of this section is repeated here to the right. The (red) circular arc within the (white) valid preferences region is again shown. The point PV may lie anywhere within this region including on its boundaries but excluding the map centre and any point above it (y > 1/3). Point PV represents the three weightings (w₁, w₂, w₃) of the chosen voting system.

The three per-unit co-ordinates of the map are a, b and c where a = w₁/Σ, b = w₂/Σ, c = w₃/Σ and Σ = w₁ + w₂ + w₃. Hence, each co-ordinate may vary within the range 0 ≤ co-ordinate ≤ 1 while simultaneously the sum of a, b and c is always unity. These three co-ordinates may therefore pinpoint both valid and invalid positional voting systems on the map.

In order to identify the geometric voting system that consistently generates the same candidate rankings as the positional voting system represented by point PV, a straight line is drawn from the map centre through point PV to the map edge at baseline P₁P₂. Point GV(r) is where this straight line intersects with the circular arc. This point represents the desired equivalent geometric voting system.

Note that, as the two points are located in different places on the map, they produce different tallies in the election. However, since both points are on the same straight line, the two systems always generate identical candidate rankings irrespective of how voters actually vote; see the previous page and both Proof CG1 and Proof CG2.

The gradient of the straight line through points PV and GV(r) is common to both points. By using this equality, the co-ordinates a, b and c for point PV and the common ratio r value for point GV(r) can all be related to the cartesian co-ordinates x and y of the map. Consequently, the common ratio r as a function of a, b and c can then be derived.

• In terms of overall candidate rankings but not tallies, any three-candidate positional voting system between plurality and the Borda Count with map co-ordinates a, b and c can be analysed or replaced by its equivalent geometric voting system where r = (b-c)/(a-b).

Substituting the three equations a = w₁/Σ, b = w₂/Σ and c = w₃/Σ into the above one for r yields r = (w₂-w₃)/(w₁-w₂). Therefore, regarding overall candidate rankings, the following geometric voting (GV) system is consistently equivalent to the proposed three-candidate positional voting (PV) system under all circumstances for any PV system between plurality and the Borda Count.

This equivalence confirms the known common ratios for CHPV, plurality and the Borda Count. For CHPV, as a = 4/7, b = 2/7 and c = 1/7, then r = (2/7 - 1/7)/(4/7 - 2/7) = (1/7)/(2/7) = 1/2. For plurality, a = 1, b = 0 and c = 0 so r = (0 - 0)/(1 - 0) = 0. For the Borda Count, a = (1+d)/3, b = 1/3 and c = (1-d)/3 where 0 < d ≤ 1. Here, r = (1/3 - (1-d)/3)/((1+d)/3 - 1/3) = 1; although strictly r only approaches 1. Note that the Borda Count is represented by every point on the straight line y = b = 1/3; namely line 1 on the preceding map on page 1. Note further that for any straight line above this line 1, there is no intersection with the circular arc and hence no valid value for the common ratio r. Also, every point on the straight line between the map centre and apex P₁ - line 3 on the preceding map - represents plurality since b = c here and r = (b-c)/(a-b) = 0/(a-b) = 0.

For positional voting elections with more than three candidates, there is usually no equivalent geometric voting system that generates identical candidate rankings under all circumstances. There are however two notable exceptions since GV(r=0) is equivalent to plurality and GV(r→1) is equivalent to the Borda Count regardless of the number of candidates competing in an election.

Proceed to next page > Comparisons: Geometric Voting 3

Return to previous page > Comparisons: Geometric Voting 1