Mathematical Proofs: Geometric Voting

Proof CG3: Identifying Equivalent Three-Candidate Voting Systems

This proof follows on from CG1 and CG2 so please refer to Proof CG1 and Proof CG2 before proceeding further. The equilateral triangular three-preference map showing the circular arc of GV systems as r varies is provided below right. The straight line y = mx + 1/3 connects the map centre (at y = 1/3 and x = 0) to the baseline P₁P₂ is also shown on this map.

As the point GV lies on the circular arc, it represents a three-candidate election that employs a geometric voting system with a specific common ratio r. This point GV also lies on the straight line at its intersection with the arc. As demonstrated in Proof CG2, all other points - such as PV - on this straight line represent positional voting systems that generate identical candidate rankings to that of the GV system.

It is therefore possible to determine the requisite common ratio r for the GV system that equates to the PV one with its three per-unit co-ordinates of a, b and c. The relationship between these co-ordinates and the cartesian ones x and y are derived in Proof CG1 and repeated here below.

For the GV system with its common ratio of r, its corresponding three map co-ordinates are a = 1/Σ, b = r/Σ and c = r²/Σ where Σ = 1 + r + r².

As the gradient (m) of the line through point PV is the same as that through point GV, then the following relationships establish the connection between the common ratio r and the three map co-ordinates a, b and c.

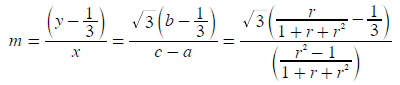
By simplifying the last relationship and solving for r, the common ratio can be evaluated.

• Therefore, in terms of overall candidate rankings, any three-candidate positional voting system between plurality and the Borda Count with map co-ordinates a, b and c can be analysed or replaced by its equivalent geometric voting system where r = (b-c)/(a-b).

Return to main text > Comparisons: Geometric Voting 2

Refer to > Mathematical Proofs: Table of Contents