Mathematical Proofs: Geometric Voting

Proof CG2: Equivalent Positional Voting Systems to Three-Candidate GV Variants

This proof follows on from CG1 so please refer to Proof CG1 before proceeding further. The equilateral triangular three-preference map showing the circular arc of GV systems as r varies is provided below right.

The weighting or cartesian co-ordinates for any point on the map, for point 1 and for point 2 respectively are given below.

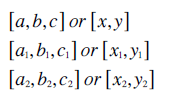
Important relationships that are derived in proof CG1 and needed here are repeated below.

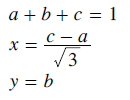
Let the weighting co-ordinates of points 1 and 2 be as stated below where ∝ is a constant.

Adding the constant (∝) to the tally of each candidate and then scaling all three tallies by the same factor of 1/(1+3∝) to re-normalise the weightings alters the absolute values of these tallies but it does not change their relative ordering. Therefore, as both points represent voting systems that generate the same collective candidate rankings, they are equivalent systems in this respect. The following four equivalences can hence be identified. The final equivalence below expresses the cartesian co-ordinates for points 1 and 2 as functions of their weighting co-ordinates.

When any two points representing equivalent systems are plotted on the map, a straight line through these two points appears to intersect the y axis at y = +1/3 (the centre of the map at point 0). To prove that this relationship is indeed valid, consider the equation for this straight line and rearrange it so that the gradient (m) becomes the subject of the equation; see below.

If each point is on the same straight line through the centre of the map, then the value of the gradient derived from point 1 must be the same as that derived from point 2; as stated below. This equality is demonstrated by substituting the weighting co-ordinate expressions of the two equivalent systems for their cartesian ones and then showing as below that the left-hand side equals the right-hand side.

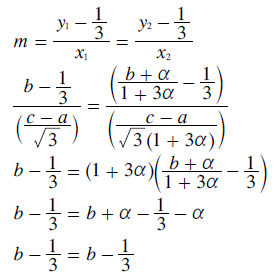
• Therefore, any two valid three-candidate positional voting systems are equivalent in ranking outcomes when the two points on the map that represent them and point 0 at the centre of the map all lie on the same straight line.

Let point 3 be the intersection of the relevant straight line with the P₁P₂ baseline; as illustrated in the above map. For GV with r = 0, the straight line intersects the apex P₁. Hence, point 3 and this apex are co-incident. As r increases towards one, the gradient of the straight line that cuts the circular arc at the relevant point tends to zero and the position of point 3 approaches one third of the distance from apex P₁ to P₂. This straight line that connects the map edge to its centre is hence horizontal and all points along it represent the Borda Count.

Return to main text > Comparisons: Geometric Voting 1

Refer to > Mathematical Proofs: Table of Contents