Evaluations: General Criteria 3

Monotonicity Criteria

For a voting system to be monotonic, it must not be possible for a voter to promote the rank of a candidate on their ballot and then consequently cause that candidate to be demoted in the election outcome rankings. Similarly, the voter must not promote a candidate overall by demoting that candidate on their ranked ballot.

In the examples opposite, one voter has promoted a candidate from second to first place by raising their own preference from fourth to third. This response is monotonic as both changes are in the same direction (promotion here). The other voter causes a candidate to be demoted from third to fourth place despite promoting their own preference from third to second. This is a non-monotonic response as the changes are in opposing directions.

Using GV/CHPV, increased weight is always added to a tally when a voter promotes the rank of candidate X and it is always subtracted from the tally when their rank is demoted instead. Provided that the relative rank order of the other candidates is unchanged, a monotonic response that ensures that X is unharmed is inherent when using any positional voting system.

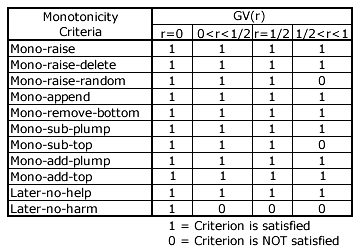
GV/CHPV hence satisfies the 'mono-raise' monotonicity criterion. This is the simplest of the various monotonicity criteria; see table opposite. Candidate X is also unharmed when the rank of X is raised on some ballots and all candidates now ranked below X on those ballots are deleted. GV/CHPV therefore satisfies the 'mono-raise-delete' criterion.

The 'mono-raise-random' criterion requires that X is unharmed when the rank of X is raised on some ballots and all the candidates now ranked below X on those ballots are ranked in any valid order including where truncation is permitted.

First consider the case of CHPV where r = 1/2. The worst case is when the rank of X is only raised by one rank position and the rank of another less-preferred candidate Y is raised from unranked to the position (with weighting w) previously occupied by X. The increase in weight gained by Y is w - 0 = w. For X, the increase is 2w - w = w. So X is unharmed and CHPV satisfies the 'mono-raise-random' criterion.

For GV in general, the increase for Y is still w - 0 = w but for X it is now w/r - w = w(1/r - 1). This bracket is less than one in value when r > 1/2 so here X is harmed. Therefore, GV with r > 1/2 fails this criterion while CHPV and GV with r < 1/2 does satisfy it. CHPV is hence the upper threshold GV variant that meets the 'mono-raise-random' criterion.

The 'mono-append' criterion is satisfied by GV/CHPV as adding X to the bottom of some ballots - when no previous preference for X was expressed - is clearly helpful rather than harmful to X. The 'mono-remove-bottom' criterion is also satisfied by GV/CHPV as removing some ballots that have X ranked bottom with all the other candidates ranked above X clearly removes less weight from X than from any other candidate so helping and not harming X.

The 'mono-sub-plump' criterion requires that X is unharmed when ballots that have X ranked below first place are replaced by ones where X is ranked top and no other preferences are expressed. As X gains in weight unlike all other candidates, this criterion is satisfied by GV/CHPV. The 'mono-sub-top' criterion requires that X is unharmed when ballots that have X ranked below first place are replaced by ones where X is ranked top and all the other candidates are ranked in any valid order including where truncation is permitted. First consider the case of CHPV where r = 1/2. Again, the worst case is when the rank of X is only raised by one rank position and the rank of another less-preferred candidate Y is raised from unranked to the position previously occupied by X; namely second place. This case is the same as that for the 'mono-raise-random' criteria except that it relates to one specific rank position (second place) rather than to any one in general. Therefore, CHPV is again the upper threshold GV variant that meets the 'mono-sub-top' criterion.

When extra GV/CHPV ballots are added and X is ranked top, then X is always helped and never harmed by these ballots. Where these ballots are truncated after the first preference, GV/CHPV then satisfies the 'mono-add-plump' criterion. Where the other candidates on these ballots are ranked in any valid order including truncation where permitted, GV/CHPV then satisfies the 'mono-add-top' criterion.

Finally, the 'later-no-help' criterion is satisfied by GV/CHPV as adding a later (lower) preference does not help any candidate that has already been given a preference. Clearly, awarding any later (weighted) preference - in contrast to using truncation and not awarding any weighting - is harmful to all candidates with prior preferences. Hence, generally, GV/CHPV does not satisfy the 'later-no-harm' criterion. The sole exception is when r = 0 as all later preferences have a zero weighting and so do not harm any earlier preferences.

Proceed to next page > Evaluations: General Criteria 4

Return to previous page > Evaluations: General Criteria 2