Map Construction: Two-Party Droop Quota Maps
Two-party (S = 2) two-winner (W = 2) scenario: Two parties A and B compete in a Droop Quota Party-List election to fill two vacant seats. Let the proportion of voters V preferring A to B be x and those preferring B to A be y; where x + y = 1. Each party nominates a closed list of its own candidates from 1 to W; where here W = 2. As explained in the main text, a tally share quota of 1/[1+W] is used to identify seat share domain boundaries on a map. For this scenario, the quota is therefore 1/[1+2] or 1/3.
All the votes for a particular party initially go to the leading candidate on the party list. Any votes in excess of the quota are then transferred to the second candidate on the list. Every candidate exceeding the quota is elected and, if a seat then remains to be filled, the candidate with the highest remaining tally share also wins. Where two candidates tie for this vacancy, this critical tie must be resolved by the random selection of one of them as the winner.
The standard election profile notation and formats are used below to state the tally and tally share for each party.
- TA = xV and tA = x for the election profile x: A1,A2.
- TB = yV and tB = y for the election profile y: B1,B2.


As the Droop Quota is a largest remainder method, bar charts can be used to display the distribution of the votes between all the candidates after the final round of counting. These bar charts are useful in determining the critical and non-critical ties for the specific election that are needed for a two-party map. Two examples are shown opposite.
The non-critical tie results when both parties A and B have an equal vote share (so x = y = 1/2) and the two seats are awarded to the prime candidate in each of the two parties. This tie represents a truly proportional outcome since both the tally share ratio and the seat share ratio are 1:1.
A critical tie occurs when the support for party A is double that for party B; where x = 2y (so x = 2/3 and y = 1/3). Note that having exceeded the quota with t = x = 2/3, A1 is the outright winner of the first vacancy. However, A2 and B1 have not exceeded the quota but merely equalled it. Since they are tied on the same 1/3 tally share, the second seat goes to either A2 or B1 selected at random. With zero tally share, B2 is the clear loser here.

If support for party A was to increase (x > 2/3) then both A candidates would be elected. Similarly, if support for party B exceeded twice that for party A, then both B candidates would win. Otherwise, when each party receives between one third and two thirds of the vote, then each party wins one seat. These three different seat ratio domains are shown on the two-party two-winner map opposite. It is the two critical ties here (at x = 1/3 and x = 2/3) that define the two boundaries between the three domains.
Two-party (S = 2) three-winner (W = 3) scenario: Two parties A and B compete in a Droop Quota Party-List election to fill three vacant seats. Let the proportion of voters V preferring A to B be x and those preferring B to A be y; with x + y = 1. Each party nominates a closed list of its own candidates from 1 to W; where here W = 3. The standard election profile notation and formats are used below to state the tally and tally share for each party.
- TA = xV and tA = x for the election profile x: A1,A2,A3.
- TB = yV and tA = y for the election profile y: B1,B2,B3.
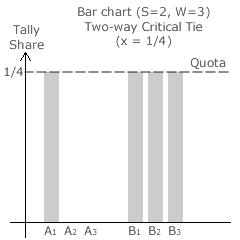
For this scenario, the quota of 1/[1+W] is 1/[1+3] or 1/4. With three winners, there are four seat share ratio domains; namely, 0:3, 1:2, 2:1 and 3:0. Hence, there are three and only three critical tie boundaries that separate them. These three two-way critical ties are shown in the adjacent bar charts. In each case, notice that every candidate either has no tally share (t = 0) or one equal to the quota (t = 1/4).
The first critical tie occurs at x = 1/4. Here, B1 and B2 take the first two seats outright with either B3 or A1 winning the third seat on a random tie break.
The second critical tie occurs at x = 1/2. Now, A1 and B1 automatically get a seat each while A2 and B2 enter the random tie breaker.
The third and only other critical tie occurs at x = 3/4. Here, A1 and A2 take the first two seats outright with either A3 or B1 winning the third seat at random.


Notice that the values of x for the three critical ties are integer multiples of the quota in the range 0 < x < 1; namely 1/4, 1/2 and 3/4. This is inevitable since four and only four candidates will share one quarter of the vote (t = 1/4) each.
Two will have won outright by exceeding the quota but they will have only retained the quota value (1/4 each) after the transfer of the excess votes.
The other two candidates (one from each party) hence share the other two quarters of the vote between them and clearly only tie for the one remaining seat when they have one quarter each.
Two-party (S = 2) multiple-winner (W = W) scenario: Two parties A and B compete in a Droop Quota Party-List election to fill W vacant seats. Let the proportion of voters V preferring A to B be x and those preferring B to A be y; so x + y = 1. Each party nominates a closed list of its own candidates from 1 to W. The standard election profile notation and formats are used below to state the tally and tally share for each party.
- TA = xV and tA = x for the election profile x: A1,A2,~~~~,AW.
- TB = yV and tA = y for the election profile y: B1,B2,~~~~,BW.
For this scenario, the quota is 1/[1+W]. With W winners, there are W + 1 seat share domains. Hence, there are only W boundaries that separate them. Here again, every candidate either has no tally share (t = 0) or one equal to the tally share quota (t = 1/[1+W]) when the critical ties occur. The values of x for the W critical ties that define the domain boundaries are again inevitably integer multiples of the quota within the range 0 < x < 1. The table below lists these domain boundary values of x for two-party scenarios with up to six winners.
| Number of Winners (W) | Quota | Domain Boundary Values of x |
|---|---|---|
| 1 | 1/2 | 1/2 |
| 2 | 1/3 | 1/3, 2/3 |
| 3 | 1/4 | 1/4, 2/4, 3/4 |
| 4 | 1/5 | 1/5, 2/5, 3/5, 4/5 |
| 5 | 1/6 | 1/6, 2/6, 3/6, 4/6, 5/6 |
| 6 | 1/7 | 1/7, 2/7, 3/7, 4/7, 5/7, 6/7 |
The two-party maps for up to six winners in a Droop Quota Party-List election are shown in the next section of the main chapter.
Return to main text > Comparisons: Party-List ~ Droop Quota
Refer to > Map Construction: Table of Contents
