Map Construction: Two-Party Sainte-Laguë Method Maps

Two-party (S = 2) two-winner (W = 2) scenario: Two parties A and B field two candidates each in a Sainte-Laguë Method Party-List election to fill two vacant seats. Let the proportion of voters V preferring A to B be x and those preferring B to A be y; where x + y = 1. For each party, its candidates are ranked from 1 to W on its closed list; where here W = 2. Candidates are identified below by their party and rank position. The standard election profile notation and formats are used below to state the tally and tally share for each party.

• T_A = xV and t_A = x for the election profile x: A₁,A₂.
• T_B = yV and t_B = y for the election profile y: B₁,B₂.

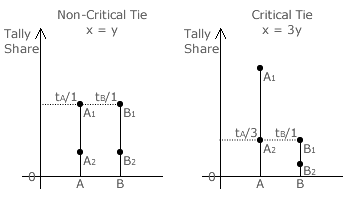
Using a party list, each party tally is therefore directly proportional to the share of the vote achieved by that party. The tally share for party A (t_A) and for party B (t_B) is hence x and y respectively. Linear party stick diagrams can now be drawn for particular values of x and y that specify critical or non-critical ties.

Two examples are shown opposite. The non-critical tie results when the two parties A and B have an equal tally share (where x = y = 1/2) since the two seats are awarded to the prime candidate in each of the two parties. A critical tie occurs when the support for party A is triple that for party B; where x = 3y (so x = 3/4 and y = 1/4).

Here, A₁ is awarded the first vacant seat and the second one goes to either A₂ or B₁ selected at random. If support for party A was to increase (x > 3/4) then both A candidates would be elected. Similarly, if support for party B exceeded triple that for party A, then both B candidates would win. Otherwise, when each party receives between one quarter and three quarters of the vote, then each party wins one seat. These three different seat share domains are shown on the two-party two-winner map opposite.

Two-party (S = 2) three-winner (W = 3) scenario: Two parties A and B field three candidates each in a Sainte-Laguë Method Party-List election to fill three vacant seats. Let the proportion of voters V preferring A to B be x and those preferring B to A be y; where x + y = 1. For each party, its candidates are ranked from 1 to W on its closed list; where here W = 3. Candidates are identified below by their party and rank position. The standard election profile notation and formats are used below to state the tally and tally share for each party.

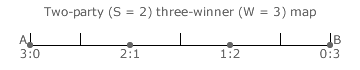
• T_A = xV and t_A = x for the election profile x: A₁,A₂,A₃.
• T_B = yV and t_B = y for the election profile y: B₁,B₂,B₃.

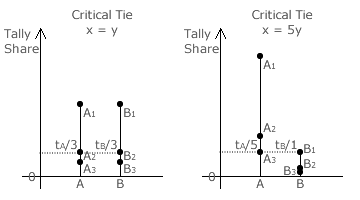
With three winners, there will be four seat share domains and three boundaries separating them. Two of the three critical ties that define these boundaries are shown opposite.

The first occurs when both parties have an equal tally share (where x = y) and the second occurs when party A has five times the support received by party B (so x = 5y). The third critical tie (not shown) is the same type as the second one except that all references to A and B are transposed (therefore y = 5x).

The resultant two-party three-winner map is shown opposite. The central domain boundary marks the 1:1 tally share ratio point on the map. The other two boundaries are located at the 5:1 and 5:1 tally share ratio points; namely at one sixth of the map length from each end. The four seat share domain dots are also included on the map.

Two-party (S = 2) multiple-winner (W = W) scenario: Two parties A and B field W candidates each in a Sainte-Laguë Method Party-List election to fill W vacant seats. Let the proportion of voters V preferring A to B be x and those preferring B to A be y; where x + y = 1. For each party, its candidates are ranked from 1 to W on its closed list. Candidates are identified below by their party and rank position. The standard election profile notation and formats are used below to state the tally and tally share for each party.

• T_A = xV and t_A = x for the election profile x: A₁,A₂,~~~~,A_W.
• T_B = yV and t_B = y for the election profile y: B₁,B₂,~~~~,B_W.

For every seat or winner added to an election, there is an additional domain and boundary to be included on the two-party map. For W winners, there are W + 1 domains and W domain boundaries; excluding the two ends of a map. By using the linear party stick diagram approach described above, all the W critical ties needed to define any two-party multiple-winner map can be derived.

For a given Sainte-Laguë Method two-party W-winner map, each of the W + 1 domains are always of the same fixed length except for the two end domains which are half the size of the others. This length is hence 1/[(W - 1)1 + 2(1/2)] or 1/W. Note the interesting equivalence here with the Hare tally share quota.

Fully completed two-party maps for up to six winners are presented in the next section of the main text.

Return to main text > Comparisons: Party-List ~ Sainte-Laguë Method

Refer to > Map Construction: Table of Contents