Map Construction: Three-Party Droop Quota Maps

Three-party (S = 3) two-winner (W = 2) scenario: Three parties A, B and C compete in a Droop Quota Party-List election to fill two vacant seats. Let the proportion of voters V preferring A be x, those preferring B be y and those preferring C be z; where x + y + z = 1. Each party nominates a closed list of its own candidates from 1 to W; where here W = 2. As explained in the main text, a tally share quota of 1/[1+W] is used to identify seat share domain boundaries on a map. For this scenario, the quota is hence 1/[1+2] or 1/3.

All the votes for a particular party initially go to the leading candidate on the party list. Any votes in excess of the quota are then transferred to the second candidate on the list. Every candidate exceeding the quota is elected and, if a seat then remains to be filled, the candidate with the highest remaining tally share also wins. Where two or more candidates tie for this vacancy, this critical tie must be resolved by the random selection of one of them as the winner.

The standard election profile notation and formats are used below to state the tally and tally share for each party.

• T_A = xV and t_A = x for the election profile x: A₁,A₂.
• T_B = yV and t_B = y for the election profile y: B₁,B₂.
• T_C = zV and t_C = z for the election profile z: C₁,C₂.

As the Droop Quota is a largest remainder method, bar charts can be used to display the distribution of the votes between all the candidates after the final round of counting. These bar charts are useful in determining all the three-way and two-way critical ties for the specific election that are needed to draw the domain boundaries on a three-party map. Five examples are shown opposite.

One obvious three-way tie is when all three parties have an equal vote share of x = y = z = 1/3. It is a critical tie as only two of the three parties will get to fill one seat each from the random tie break.

A two-way critical tie occurs when x exceeds 1/3 and y and z share the remainder equally. Here, A₁ gains the first seat outright and either B₁ or C₁ gets the second following the tie break. This y = z two-way tie continues as x rises by 2/9 from 1/3 to 5/9.

At this point another three-way critical tie occurs; namely x - 1/3 = y = z. So A₁ still wins the first seat but here an excess of 2/9 (above the 1/3 quota) is transferred to A₂. As B₁ and C₁ share the remainder, they too each have a tally share of 2/9. Hence, the second seat is randomly awarded to one of these three candidates.

Another two-way critical tie occurs when z now decreases but with A₂ and B₁ still sharing the remaining tally share. Here, the tie is x - 1/3 = y. This critical tie continues until z = 0 and x = 2y. This point is hence on the edge of the map where x = 2/3 and y = 1/3. A₁ still retains the first seat but now A₂ and B₁ compete in the random tie break for the second seat.

For the two-winner (W = 2) map, both types of the three-way critical ties and both types of the two-way ones have now been identified. For more than two winners, there will be increasing numbers of tied-situation types but for W = 2 there are no further types.

The four specific critical ties shown in the first four bar charts are drawn on the map below left. [The fifth bar chart simply illustrates the case where the second two-way tie line meets the map edge.] The three-way critical ties are shown as small dots. The central one is where candidates A₁, B₁ and C₁ have an equal tally share and the one above is where A₂, B₁ and C₁ have an equal tally share.

The two-way ties are shown as lines since the tally share of the non-tied party can vary (between certain limits). Hence, all points along a two-way tie line represent critical ties. The y = z tie line connects the two three-way tie dots on the map. The x - 1/3 = y tie line emanates from the upper dot and terminates when it reaches the map edge where x = 2y and z = 0. It is important to note that this tie line is at right-angles to the edge of the map since x and y change by the same amount as z varies.

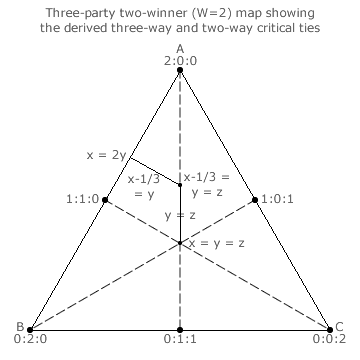
On the completed three-party two-winner map above right, all nine two-way critical tie lines are shown. These lines hence form the unique seat share domain boundaries for this election. Each of the four three-way critical ties is at the junction where three two-way tie lines meet. Alternatively stated, each three-way critical tie is where three adjacent domains meet.

Each of the three dashed lines in the map above left bisects the triangle in half and each half is the mirror image of the other. Therefore, the six ranking regions that result from the three bisections are all symmetrical to each other. This hex-symmetry means that only the three-way and two-way critical ties in one of the six ranking regions must be identified; as shown. The others will be of exactly the same type (with just the relevant candidates transposed) and simply be reflections of this initial region. So, flip any base or rotate the map through one third of a cycle and the lines on the map will be identical.

Three-party (S = 3) three-winner (W = 3) scenario: Three parties A, B and C compete in a Droop Quota Party-List election to fill three vacant seats. Let the proportion of voters V preferring A be x, those preferring B be y and those preferring C be z; where x + y + z = 1. Each party nominates a closed list of its own candidates from 1 to W; where here W = 3. The standard election profile notation and formats are used below to state the tally and tally share for each party.

• T_A = xV and t_A = x for the election profile x: A₁,A₂,A₃.
• T_B = yV and t_B = y for the election profile y: B₁,B₂,B₃.
• T_C = zV and t_C = z for the election profile z: C₁,C₂,C₃.

With an extra winner in this scenario, there will be additional critical ties to consider. However, by identifying the two-way ones first, the three-way ones will automatically appear as they result from the junction of three two-way ties. For two winners, the quota is 1/3 and the tie lines that meet the map edge at right-angles do so at intervals of this fraction along the map edge. For three winners, the quota is 1/4 and the tie lines now meet the map edges at intervals of 1/4.

For the inner two-way critical tie lines, they occur along lines that are intermediate between and parallel to the outer ones. Therefore, all two-way critical ties are coincident with grid lines at right-angles to a map edge and spaced at intervals of 1/8 along each map edge; as shown in the map below left.

All that needs to be determined now is which sections of a grid line are critical and which are not. This is done using the bar charts as described above. However, due to hex-symmetry, only one of the six regions should be analysed as the other five are mere reflections of it. Once this analysis is complete and the critical two-way ties are known, these resultant domain boundaries can be redrawn as full lines and the non-critical sections deleted; as shown in the map above right.

Three-party (S = 3) multiple-winner (W = W) scenario: Three parties A, B and C compete in a Droop Quota Party-List election to fill W vacant seats. Let the proportion of voters V preferring A be x, those preferring B be y and those preferring C be z; where x + y + z = 1. Each party nominates a closed list of its own candidates from 1 to W. The standard election profile notation and formats are used below to state the tally and tally share for each party.

• T_A = xV and t_A = x for the election profile x: A₁,A₂,~~~~,A_W.
• T_B = yV and t_B = y for the election profile y: B₁,B₂,~~~~,B_W.
• T_C = zV and t_C = z for the election profile z: C₁,C₂,~~~~,C_W.

With more winners, there will be further two-way tie lines to draw on the map. For W winners, the quota is 1/[1+W] and grid lines should now be drawn at right-angles to the map edge at intervals of half this value along each map edge. As always, bar charts can then be employed to identify the critical and non-critical sections of these grid tie lines. The critical sections should be shown as full lines and the non-critical ones deleted. Also, as always, only one of the hex-symmetrical regions need be analysed to derive the domain boundaries. The complete three-party map for any number of winners can therefore be produced quite easily using this standard approach.

The three-party maps for up to six winners in a Droop Quota Party-List election are shown in the next section of the main chapter.

Return to main text > Comparisons: Party-List ~ Droop Quota

Refer to > Map Construction: Table of Contents