Mathematical Proofs: Borda Count

Proof CB1: Candidate Preferences and Average Rank Positions

For Borda Count elections, let the common difference between adjacent preferences be one point and the weighting of the lowest (last) preference be L points. The number of candidates is N and the number of voters is V. Also, let the number of voters awarding an nth preference (with a weighting of w_n) to a candidate be x_n. The following list defines the Borda Count weightings used in this election.

• w₁ = N - 1 + L
• w₂ = N - 2 + L
• w₃ = N - 3 + L
• w_n = N - n + L
• w_N = N - N + L = L

Where truncation does not occur, all voters award one preference to each candidate. Hence, regardless of the rank of any preference, the total number of preferences received by each candidate is equal to the total number of votes cast; as stated below.

The tally (T) for any candidate is the sum for all N preferences of the products of the number of nth preferences awarded and their weighting; as stated below. The average tally per voter (T_AV) for a candidate is simply their tally divided by the total number of voters; as follows.

The average rank position (n_AV) of a candidate is defined as the vote-weighted (x-weighted) average value of the rank position (n); as stated below.

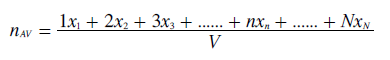
The following derivation simplifies the sum of the average tally per voter (T_AV) for a candidate and their average rank position (n_AV).

For any given election, the number of voters (V), the number of candidates (N) and the weighting of the lowest preference (L) are all fixed. The collective ranking of the candidates from first to last is determined by the descending order of the candidate tallies. Dividing all such tallies by V to produce the average tally per voter does not alter this ranking when using these averages instead of the absolute tallies to determine the results.

As N + L is a constant, this means that as T_AV rises n_AV falls by the same amount. So, the highest T_AV and the lowest value of n_AV belong to the top-ranked (winning) candidate. The next highest T_AV and the next lowest value of n_AV belong to the second-ranked candidate and so on. Note that the lower of two values of n_AV has the higher rank. For example, an average rank position of two (second place) is higher in rank order than three (third place). Therefore, the following two statements are true for any Borda Count election where truncation does not occur.

• As an alternative to the descending order of candidates tallies, the ascending order of candidate average rank positions can be used instead to list candidates in collective descending rank order.
• To win, a candidate requires an average rank position that is lowest in value and hence highest in rank.

Return to main text > Comparisons: Borda Count 1

Refer to > Mathematical Proofs: Table of Contents