Mathematical Proofs: Geometric Voting

Proof CG4: Iso-Tally Grid Lines on Three-Candidate Maps

For each candidate in a three-candidate election that uses positional voting, their share of first, second and third preferences can be plotted on a three-candidate map; see opposite. Every candidate receives a preference of some weight from each voter as truncation is not permitted here.

Let the number of first preferences (P₁) cast for a particular candidate be V₁, the number of second preferences (P₂) be V₂ and the number of third preferences (P₃) be V₃. The sum of these numbers must hence equal the number of voters (V). Dividing V₁, V₂ and V₃ by V yields the share of first, second and third preferences received by a candidate.

These per-unit shares (v₁, v₂ and v₃) necessarily sum to unity and can hence be represented on an equilateral triangular map. Such a map is very similar in construction and use to the Three-Party CHPV Maps described in the Map Construction appendix. Here however, each apex represents a full share for the stated preference and no share for the other two. For example, apex P₁ represents a candidate with a first preference from every voter.

As GV can represent any three-candidate positional voting system, then let GV with a common ratio of r be the method employed in the election.

For convenience, let the first preference be worth one so that the second and third preferences are worth r and r². As shown below, the tally (T) for a candidate is then simply the sum of the total number of each preference times its own weighting. Dividing T by V yields the average tally per voter (t) and it is this value that any point on the map represents. The division by V for each candidate tally does not alter the collective candidate rankings as the rank order of the T and t values are identical. The derivation that follows derives the relationship between the share of first and third preferences for a given value of r and t.

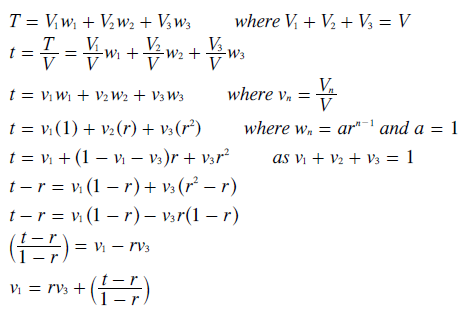
Grid lines where every point along such a line has the same value for the average tally per voter (t) are called iso-tally lines. To prove that such lines are parallel straight lines when plotted on the map it is convenient to use conventional cartesian co-ordinates (x,y) rather than the preference share co-ordinates (v₁,v₂,v₃). The cartesian origin of the map is at the mid-point of the P₁P₃ baseline. Bearing in mind that the map is an equilateral triangle of unit perpendicular height, the x and y co-ordinates of each apex are defined below left. The straight line equation for each baseline is also given; below right.

As each preference share varies from zero at its baseline to one at its apex, then the scaling constant k for each preference share can be determined as shown below.

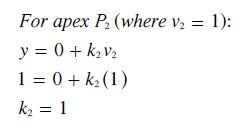
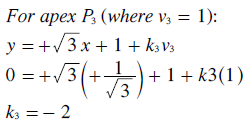
Substituting these three values for k back into their original equations yields the relationships between the x,y and v₁,v₂,v₃ co-ordinates; see below. Clearly, as intended, the y and v₂ co-ordinates are one and the same.

By rearranging these three equations, the transform equations for each of the three preference share co-ordinates in terms of x and y are derived; see below.

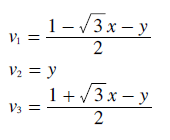
The above expressions for v₁ and v₃ can then be substituted into the equation (derived above) that defines the relationship between v₁ and v₃; see below. The derivation that follows demonstrates that y is indeed a straight line function of x.

The primary iso-tally grid line is defined as the one where the average tally per voter (t) is equal to the weighting of the second preference (r). This primary iso-tally line always intercepts the y-axis at apex P₂ as c = 1 for t = r regardless of the specific value of r; see below. This is not surprising since apex P₂ represents a candidate with a second preference from every voter and so an average tally of r per voter.

Notice that the relationship between the first and third preference shares can be simplified for the primary iso-tally line; see equation above. The ratio of first to third preference shares is now equal to the GV common ratio (r). The intercept of the primary iso-tally line with the P₁P₃ baseline is easily determined as the tally scale along it is linear; as demonstrated in the following analysis. The primary iso-tally line intercepts this linear scale (from r² at apex P₃ to 1 at apex P₁) at r; since t = r for this line. This primary line is shown in bold on the above map.

Hence, t is proportional to v₁ for any given r.

• The primary iso-tally grid line (where t = r) is a straight line between apex P₂ and the point on the linear P₁P₃ baseline whose value is r.

Notice that the gradient (m) in the earlier general equation for any iso-tally line is only a function of r. Hence, for any given value of r, the gradient is fixed. This means that any iso-tally line has the same gradient as the primary one. In other words, the two lines are parallel. Therefore, the following statement is always true.

• Any secondary iso-tally grid line for tally t is parallel to the primary one and intercepts the linear P₁P₃ baseline at the point whose value is t.

Iso-tally grid lines for specified values of t can now be drawn on the map for a three-candidate GV election with a particular value of the common ratio (r). In the example CHPV (GV with r = 1/2) map opposite, iso-tally grid lines for values of t from 1/4 to 1 in steps of 1/12 are shown. The primary grid line where t = r = 1/2 is shown in bold.

Return to main text > Comparisons: Geometric Voting 4

Refer to > Mathematical Proofs: Table of Contents