Mathematical Proofs: Geometric Voting

Proof CG5: Minimum Winning Rank for a Consensus Candidate

Scenario: There are V voters in a single-winner election with N candidates. One candidate receives the nth preference from every voter and is hence referred to as the consensus candidate C. The tally for C is then simply V times the weighting of the nth preference (w_n); as stated below. All the remaining (N-1) candidates receive an equal share of each of the other (N-1) preferences. Therefore, each such candidate has the same number of first, second and other preferences (except the nth) as the other non-consensus candidates. These N-1 candidates have equal tallies and are critically tied when ranked above the consensus candidate. Let one of these tied candidates (with the evenly distributed preferences) be D. The tally for D is derived below.

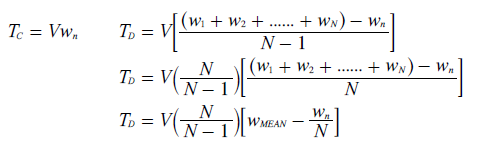
For the consensus candidate C to gain victory in the election, the tally for C must be greater than the tally for D. The criterion for this victory is derived below.

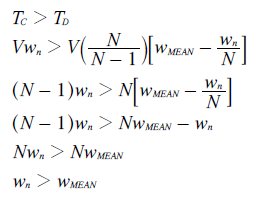
• Hence, the minimum winning rank of the preference awarded to the consensus candidate is always greater than the rank of the preference with the mean weighting.

If the non-consensus candidates have any other distribution of the preferences awarded to them (that is, an unequal one), then they will not all be tied. Some will then have higher tallies and others lower ones. It will now be even more difficult for the consensus candidate to beat the top-ranked one.

• In other words, a candidate with a unanimous preference from every voter can never win when the rank of this preference is lower than the mean-weighted one.

Return to main text > Comparisons: Geometric Voting 6

Refer to > Mathematical Proofs: Table of Contents