Mathematical Proofs: Positional Voting

Proof CV1: Consensus and Polarization Indices for Positional Voting Vectors

The consensus index (CI_V) for a positional voting vector is defined as the weighted average of all the individual consensus indices (CI_L) for the lower preference in each adjacent pair of preferences. The higher preference in each pair is employed to weight these indices in every case. The CI_V is therefore calculated as follows.

The polarization index (PI_V) is similarly calculated using all the individual polarization indices (PI_L) instead; as follows.

As CI_V and PI_V should sum to one, the following check confirms this relationship.

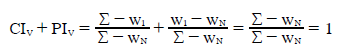
For vectors normalized such that w₁ = 1 and w_N = 0, the two vector bias indices may be simplified further as shown below.

The polarization index is simply the reciprocal of the sum of all the normalized preference weightings.

Return to main text > Comparisons: Positional Voting 2

Refer to > Mathematical Proofs: Table of Contents