Mathematical Proofs: Clones, Teaming and Independence Criteria

Proof EC1: GV (any r) is not Independent of Irrelevant Alternatives

Scenario: Three candidates A, B and C contest a ranked ballot GV election. The common ratio may be any value in its range of 0 ≤ r < 1. Let v + x, v and v - y be the number of ranked ballots of the same type cast by the appropriate group of voters. Using standard notation and formats, the profile for this election scenario is given below.

• v+x: A,B,C. where 0 < x
•   v : B,C,A. where 2 < v
• v-y: C,A,B. where 0 < y < v

The standard GV weightings are used here to determine the tallies (T) for candidates A, B and C. The conditions for A beating B, A beating C and B beating C are then derived as shown below.

As the above two conditions relating to candidate C are always TRUE regardless of the value of r, then A beats C and B beats C for all r. However, the ranking of A and B depends on the value of r as stated below.

• Case 1: For r < x/y, A beats B with C last
• Case 2: For r = x/y, A and B tie with C last
• Case 3: For r > x/y, B beats A with C last

Case 1: Candidates B and C both lose. By taking B as the irrelevant alternative, now consider the effect of the withdrawal of B from the election by rerunning it without B yet maintaining the relative preference of every voter for A over C or the reverse. The rerun election profile is given below.

• v+x: A,C. where 0 < x
•   v : C,A. where 2 < v
• v-y: C,A. where 0 < y < v

The rerun candidate tallies and ranking conditions are derived as shown below.

Notice that the condition for A beating C is not a function of r (for this case 1). It is easy to allocate values to this condition such that it is FALSE; for example, where x = 1, y = 1 and v ≥ 3. Hence, for all 0 ≤ r < x/y, C can beat A. Therefore, as A can fail to win the election merely as a result of a losing and irrelevant candidate (B) withdrawing from the contest, then the independence criterion is not satisfied for case 1.

Case 2: A fails to win as B ties with A here. Case 3: A fails to win as B beats A. In both cases, A fails to win and C is a losing and irrelevant candidate. Now consider the withdrawal of C from the election by rerunning it without C yet maintaining the relative preference of every voter for B over A or the reverse. The new rerun profile is given below.

• v+x: A,B. where 0 < x
•   v : B,A. where 2 < v
• v-y: A,B. where 0 < y < v

The new rerun candidate tallies and ranking conditions are derived as shown below.

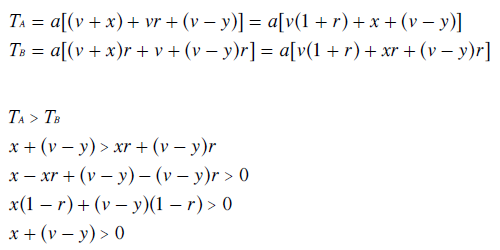
Notice that the condition for A beating B is not a function of r (for cases 2 and 3). Also, as x and v - y are both positive, then this condition is always TRUE. Hence, for all x/y ≤ r < 1, A beats B. Therefore, as A now wins the election (where previously A did not) merely as a result of a losing and irrelevant candidate (C) withdrawing from the contest, then the independence criterion is not satisfied for case 2 or 3.

Cases 1, 2 and 3: For every case of this election profile and for all valid values of r, the withdrawal of an irrelevant candidate can overturn the outcome of the single-winner contest. There are numerous other profiles that produce similar upsets. Hence, GV (any r) is not Independent of Irrelevant Alternatives.

Return to main text > Evaluations: Clones & Teaming 1

Refer to > Mathematical Proofs: Table of Contents