Mathematical Proofs: General Criteria

Proof EG3: GV (any r) fails the Reversal Symmetry Criterion

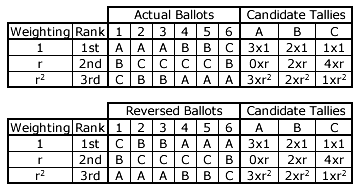
Scenario: Three candidates A, B and C are nominated for a single-winner GV (any r) election in which six voters cast their three preferences as stated in the upper table opposite. The resultant candidate tallies (T) are therefore as follows:

• T_A = 3 + 3r²
• T_B = 2 + 2r + 2r²
• T_C = 1 + 4r + r²

Now consider the case where the strict rank ordering of the three preferences on each of the six ballots is reversed as stated in the lower table opposite. Notice that the candidate tallies here are identical to the ones above. Therefore, the election result is in no way altered by this reversal.

GV would not meet the reversal symmetry criterion where one candidate (A here) is still the winner when all the ballots have reversed preferences. To prove that A does win before and after the reversal, the tally for A must be greater than the tally for B and the one for C. The two equations are defined and simplified below.

The two simplified equations above are in fact identical. Therefore, if this tally comparison equation is true for any valid value of r, then GV does not satisfy the reversal symmetry criterion. This equation is further simplified below.

As x is a non-zero positive number (no higher than one), then x² is also a non-zero positive one and the above equation is always true. Hence, for any valid value of r, the tally for A is invariably greater than that for either B or C so candidate A always wins whether the ballots are reversed or not.

• Therefore, GV (any r) fails the reversal symmetry criterion.

Return to main text > Evaluations: General Criteria 2

Refer to > Mathematical Proofs: Table of Contents