Mathematical Proofs: Optimality of CHPV

Proof EO2: Extreme Seat Share Domain Volume Ratios for CHPV Maps

Domain to Map Ratios for Two- and Three-Party Contests

The three-party map below shows one of the three corner domains. This domain is where all the winners (W in total) belong to the same party and the others fail to win a single seat. Hence, such domains are called 'extreme seat share' ones. Any edge of the three-party map equates to a two-party map as the relevant third party has zero votes. The labeled lengths on the map are defined below.

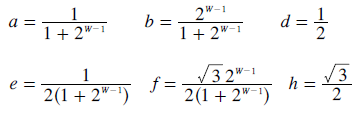
By defining the tangent of angle * for the two different right-angled triangles sharing this angle, the height c can then be deduced as shown below.

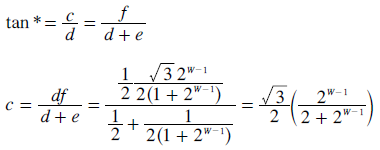
For the two-party map with W vacancies for the winners, the boundary of the end domain equates with one party having the first W-1 seats and the two parties tying for the last remaining one. This occurs when the tally share ratio is 2^W-1:1 and hence lengths a and b are also in this ratio while summing to unity. So for S = 2, the ratio between domain length and map (edge) length is given opposite.

For the three-party map, the extreme seat share domain is formed by two map edge sections and two boundary sections with a constant 2^W-1:1 ratio between the relevant two party tally shares. The area of the domain is simply half of the width times the height. Therefore for S = 3, the ratio between domain area and map area is given below.

Domain to Map Ratio for Four-Party Contests

For a four-party contest, the solid map is a regular tetrahedron with four equilateral triangles as its faces and where each side is of length 'a'. A plan view is shown below with the base face furthest from the observer and the opposing apex (2) nearest. A central and vertical cross-section through this tetrahedron is also shown below. The length 'b' corresponds to the perpendicular height of its triangular face; namely (√3/2)a.

The area of the triangular cross-section is half the base times the perpendicular height. By computing this area two different ways, the unknown height 'h' can be determined as shown below. The volume of any tetrahedron can be determined as a function of 'a' and 'h'; see below again. Finally, as 'h' is now known, the volume of any regular tetrahedron can be determined as a function of just 'a'; see below once more.

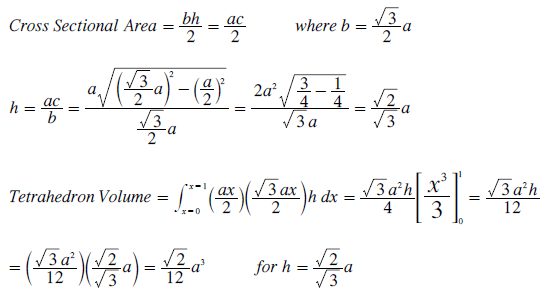
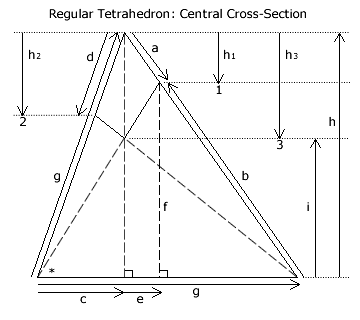
A detailed view of the central cross-section is shown opposite. The extreme seat share domain boundary meets the right-hand edge at distance 'a' from the top apex and the left-hand edge at distance 'd' from it. This distance 'd' is the height of the extreme domain on the S = 3 triangular map (see earlier above) as measured along the vertical centre line. Other relevant distances are given below.

Before being able to calculate the volume of the domain, the heights h₁ and h₃ must be deduced. The actual value of h₂ is unimportant. Height h₁ is simply the perpendicular component of the vector length 'a'. By taking the tangent of angle * in two different right-angled triangles, the height 'i' can be derived. Height h₃ is then simply h - i. All calculations are also shown below.

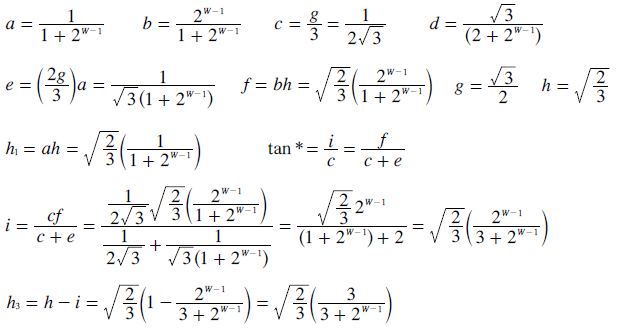
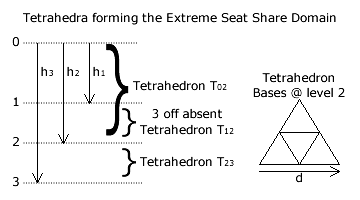
Each solid extreme seat share domain comprises two tetrahedra with three corner tetrahedra removed from the upper one. In the diagram opposite, the upper tetrahedron T₀₂ has its apex at the top of the map (level 0) and its base at level 2. The side length of this base is 'd' as it is the same distance 'd' along the edge of the regular tetrahedron T₀₂; see cross-sectional view above.

The base of T₀₂ can be partitioned into four congruent triangles as shown. The three small corner triangles are the bases of the regular tetrahedra T₁₂ that do not form part of the domain and are absent from its volume. Each of these three tetrahedra have their apex at level 1. The remaining central small triangle is the base of tetrahedron T₂₃ that has its apex at level 3.

The area of a triangular base is half of the side length times the perpendicular height (= √3/2 side length). The side length for T₀₂ is d and for T₁₂ and T₂₃ it is d/2. The equations for the base areas are given below.

The volume of a tetrahedron is one third of its base area times its height. The domain volume is the volume of tetrahedron T₀₂ with the three small tetrahedra T₁₂ removed but together with the small tetrahedron T₂₃ added underneath. This domain volume is calculated below. The map volume is already determined above as √2/12 times the cube of the map edge length (=1³). Finally, the ratio of the domain volume relative to the map volume is derived as shown below.

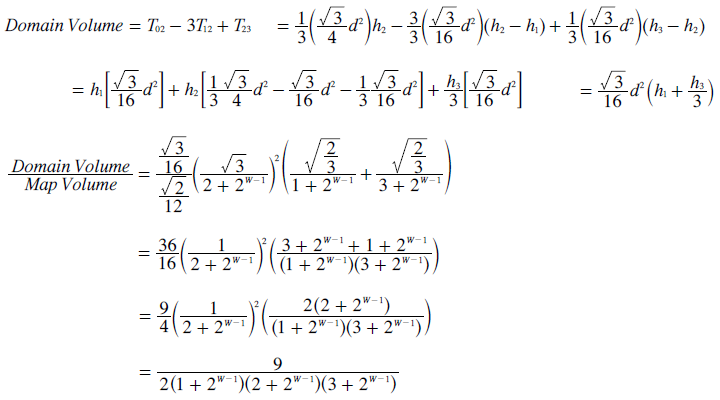
This extreme seat share domain to map volume ratio for four-party (S=4) contests is listed in the table in the main text; together with the equivalent ratios for two-party (S=2) and three-party (S=3) elections as determined above.

Comparison of CHPV to OPV Extreme Seat Share Domain Volume Ratios

In order to compare the relative size of the two extreme seat share domains, another ratio is again taken. This ratio is the volume (or area or length) ratio of the CHPV domain relative to the volume (or area or length) ratio of the OPV domain. The closer that this CHPV/OPV ratio is to one, then the closer CHPV will be to OPV in terms of optimality. The domain volume ratios for two-, three- and four-party CHPV elections (derived above) and the equivalent OPV ones (see proof EO1) are used as shown below to determine the three comparative CHPV/OPV ratios.

Notice that these ratios have not been fully minimised in order that the pattern that emerges with every extra party added is clearly visible. These ratios are listed in the right-hand column of the table in the main text.

Return to main text > Evaluations: Optimality 3

Refer to > Mathematical Proofs: Table of Contents