Mathematical Proofs: Teaming Thresholds

Proof ET4: GV Teaming Thresholds for Clone Set versus Many Candidates

Scenario: The election is conducted using GV and its standard weightings are used here to determine the tally (T) for any of the N candidates on the ballot. The weighting of the first preference is set at one (w₁ = a = 1) and the number of voters casting valid ballots is V. The clone set is A and it nominates K clones in total. On its forward slate, its clones are listed from A₁ to A_K. The reverse slate therefore lists these clones from A_K to A₁ in exactly the reverse sequence. In this final and general scenario, an unlimited number of candidates M (where N = K + M and M > 0) have been nominated to oppose the clone set A. All voters rank the clone candidates in either forward or reverse order.

• p_F = Of those preferring A first, the proportion who rank the clone set in forward slate order
• p_R = Of those preferring A first, the proportion who rank the clone set in reverse slate order
• q_F = Of those not preferring A first, the proportion who rank the clone set in forward slate order
• q_R = Of those not preferring A first, the proportion who rank the clone set in reverse slate order

Hence, for those preferring A first, p_F + p_R = 1 and, for those not preferring A first, q_F + q_R = 1. Where all first preference A voters rank candidates in compliance with the forward slate, p_F = 1 and p_R = 0. Where they vote consistently for the reverse slate, p_R = 1 and p_F = 0. If no slate is issued and all clones are identical rather than fraternal, then p_F = 1/2 and p_R = 1/2. The same holds for all other first preference voters except that the proportion p is now replaced by the proportion q.

For the clone set, there is no point in teaming if it would win anyway with just one candidate A. Therefore, its easiest opportunity to win unfairly through teaming is when it is tied with all the other competing candidates (M in total). This pre-cloning critical tie between all candidates is where each has one Nth of first preferences, one Nth of second preferences and one Nth of every other rank preferences. Hence, the tally for A (T_A) equals the tally for any other single candidate (T_M). After nominating its K clones, the tally for either A₁ (T_A1) or A_K (T_AK) must exceed the common tally (T_M) for each of the other candidates for successful teaming to occur.

Given the unlimited number M of candidates, it is no longer possible to list all the different ballot types used within the election profile. Instead, the equations for the relevant tallies must be deduced from the developing patterns exhibited within and across the three previous proofs; ET1 where M = 1, ET2 where M = 2 and ET3 where M = 3. The initial tally for T_M is given below.

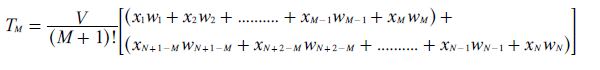
Prior to cloning, there are M + 1 candidates so after cloning there are 2 x (M + 1)! permutations of ranked ballots. These ballot types always come in pairs as one specifies a forward slate and the other a reverse slate. For each of the M candidates, the slate direction makes no difference so these pairs can be combined (as p_F + p_R = 1 and q_F + q_R = 1). The quantity of votes cast for each pair is the same due to the tied preferences. Hence, this quantity is V / (M + 1)! as each has an equal share of V votes. Each of the M candidates receives a number (x_n) of weightings (w_n) towards its tally from the first M rank positions and also from the last M places. The table below shows the x coefficients needed to calculate the tally T_M.

The coefficients already used for M = 1, M = 2 and M = 3 have simply been transferred directly into this table. The ones for M = 4 and M = 5 have also been worked out from the relevant (and lengthy) election profile and entered into the table. Fortunately, the pattern of coefficients that emerge as M increases is easy to deduce. For M = 4, the four coefficients are consecutive integer multiples of 6 where 6 is the factorial of one less than 4. For M = 5, the five coefficients are consecutive integer multiples of 24 where 24 is the factorial of one less than 5 (as shown in the penultimate row). Therefore, for M = M, the M coefficients are consecutive integer multiples of (M - 1)! (as shown in the final row). By substituting these coefficients into the initial tally above the resultant one is as stated below.

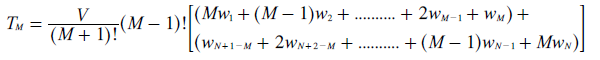
Now consider the tally for candidate A₁ (T_A1). The initial equation is given below. As before, each pair of ballot types receives a total of V / (M + 1)! votes.

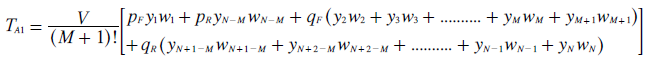
However, A₁ leads on the forward slate and trails on the reverse one so ballot types here cannot be considered in pairs. For forward slates, A₁ is ranked first by A supporters and somewhere in the following M rank positions by the other voters. For reverse slates, A₁ is ranked in Kth place (where K = N - M) and somewhere in the bottom M places by the other voters. Candidate A₁ receives a number (y_n) of weightings (w_n) towards its tally from these rank positions. Each product term (y_nw_n) must be multiplied by its appropriate p or q proportion. The table below shows the y coefficients needed to calculate the tally T_A1 and the relevant p or q proportion at the bottom of each column.

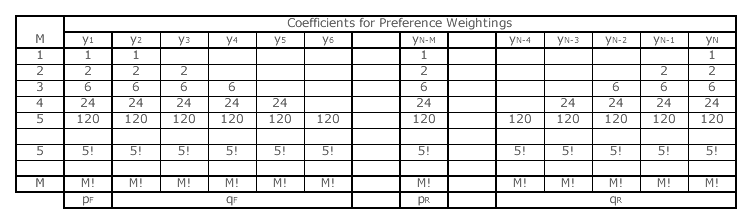
The coefficients already used for M = 1, M = 2 and M = 3 have simply been transferred directly into this table. The ones for M = 4 and M = 5 have also been worked out from the relevant (and lengthy) election profile and entered into the table. Fortunately, the pattern of coefficients that emerge as M increases is again obvious. For M = M, all coefficients are simply equal to the factorial of M (M!). By substituting these coefficients into the initial tally above and then substituting (1 - p_R) for p_F and also (1 - q_F) for q_R, the resultant one can be derived as shown below.

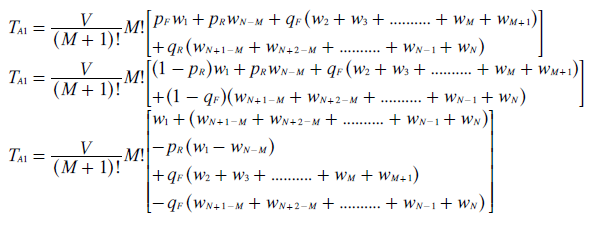
For clone A₁ to win through cloning, the tally for A₁ must exceed the one for any of the M candidates; namely T_A1 > T_M. To maximise the tally for A₁, clone set A should issue a forward slate to minimise the value of p_R. To minimise this same tally, supporters of the M candidates should reverse the slate to minimise the value of q_F. By evaluating the tallies for A₁ and M, this key relationship between q_F and p_R - the teaming threshold for A₁ - can be derived as shown below.

Notice that for every bracket containing a difference between two weights, each can be replaced by rⁱ(w₂ - w_N+1-M) with the appropriate value of i inserted since such differences reflect an identical separation distance between their rank positions. For example, w₃ - w_N+2-M can be substituted by r(w₂ - w_N+1-M) as by definition w_N+1 = rw_N. Hence, by dividing both sides of the equation by w₂ - w_N+1-M, this equation can be greatly simplified as demonstrated below.

The above teaming threshold determines the relative ranking of A₁ and the M tied candidates as follows.

• For q_F > teaming threshold, A₁ wins through successful teaming against all M candidates.
• For q_F = teaming threshold, all M candidates and A₁ are still tied.
• For q_F < teaming threshold, all M candidates jointly beat A₁ through vote splitting.

For clone A_K to win through cloning, the tally for A_K must exceed the one for any of the M candidates; namely T_AK > T_M. By evaluating the tallies for A_K and M, the key relationship between q_R and p_F - the teaming threshold for A_K - can be derived in exactly the same manner as above but with the _F and _R subscripts for p and q exchanged. This relationship is stated below.

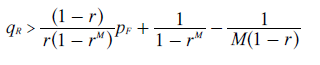
The above teaming threshold determines the relative ranking of A_K and the M tied candidates as follows.

• For q_R > teaming threshold, A_K wins through successful teaming against all M candidates.
• For q_R = teaming threshold, all M candidates and A_K are still tied.
• For q_R < teaming threshold, all M candidates jointly beat A_K through vote splitting.

Note that to beat A and remain tied in first place, the M candidates must simultaneously beat both A₁ and A_K.

Return to main text > Evaluations: Teaming Thresholds 3

Refer to > Mathematical Proofs: Table of Contents