Evaluations: Majority and Related Criteria 3
Consensus versus Polarized Candidates
Apart from one special case, GV does not satisfy the majority criterion. This raises the prospect of a consensus candidate C 'coming through the middle' to beat two polarized candidates A and B. Let m remain the proportion of voters casting a first preference (P1) for A while the remaining proportion of 1 - m cast a first preference for B. If C receives a second preference from every voter, can C win despite having no first preferences at all? Following a pairwise comparison of the GV tally (T) for every pair of candidates, the answer is yes! The ranking thresholds for such an election are given below.
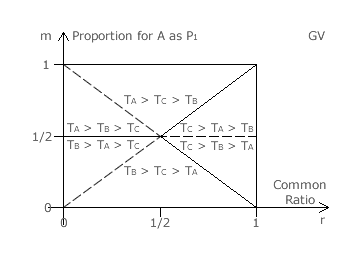
The above three threshold conditions are each represented on the graph opposite by a straight line. The solid half of each line is the threshold between the first- and second-ranked candidates exchanging places and the dashed half is between the second- and third-ranked candidates swapping places. Each threshold line represents a tie between two candidates and the single point at which all three lines cross represents the only three-way tie between A, B and C. This three-way tie only occurs when using CHPV (r = 1/2).
The white region of the graph is where the tally for C is greater than for either A or B and hence where C wins. It is clear from this graph that for common ratios less than one half (r < 1/2), C can never win. However, for common ratios greater than one half (r > 1/2), C might easily win. The chances of C winning are best when the polarization between A and B is well balanced and they improve steadily as the common ratio is increased. A common ratio of one half is therefore the threshold below which a consensus candidate with unanimous second preference support cannot beat the leading candidate of two who share all the first preferences between them.
CHPV is therefore the boundary GV variant for a consensus candidate with no first preference support to be able to 'come through the middle' and beat two polarized candidates sharing such support. Using CHPV in practice, a candidate with almost universal second preference support must have at least one first preference to stand any chance of being elected (without winning a tie-break). This chance improves as more first preferences are accumulated and when the polarization between the other two candidates becomes more evenly balanced.
Proceed to next page > Evaluations: Majority Criteria 4
Return to previous page > Evaluations: Majority Criteria 2
