Evaluations: Majority and Related Criteria 4

Strong versus Broad Support

Voters in a GV election cast first preferences to show their strong support for a candidate. The candidate with the strongest support is the one with the most first preferences. In contrast, broad support from across the electorate is where a candidate receives a large proportion of preferences that are of relatively high rank. Where truncation is not permitted, such support may be quantified as the mean rank position of all the preferences awarded to a candidate . The one with the broadest support is the candidate having the highest mean rank position.

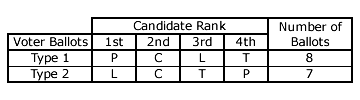
Consider an example GV election in which four candidates compete for votes in an electorate of fifteen voters. The ranked ballots are cast according to the table shown opposite. The polarized candidate P has the strongest support with a plurality and marginal majority of the first preferences. The consensus candidate C has the broadest support as it has the highest mean rank position. By summing the fifteen rank positions and dividing by fifteen, this mean is thus calculated. The mean rank positions for the four candidates are therefore 2, 2.067, 2.4 and 3.533 for C, L, P and T respectively.

Of the other two challenger candidates, the leading one L is preferred to the trailing one T by every voter. Hence, candidate T can never win this election regardless of the common ratio employed. The support for the leading challenger L is almost as strong as for the polarized candidate P and almost as broad as for the consensus candidate C. With a good combination of both relatively strong and broad support, is it possible for L to simultaneously beat both P and C and so win the election? Also, if yes, what range of common ratios enables L to win?

• The resultant tallies (T) as a function of the common ratio (r) for this example election are shown in the graph opposite and the collective candidate rank orders for four specific cases are listed below.

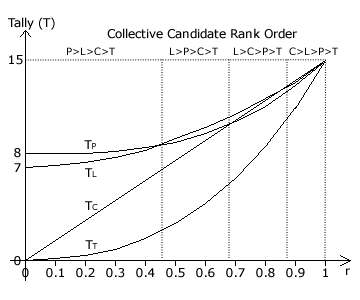
• P > L > C = T for GV(r=0)
• L > P > C > T for GV(r=1/2) = CHPV
• L > C > P > T for GV(r=3/4)
• C > L > P > T for GV(r→1)

This example election indeed demonstrates that the winner requires strong support, broad support or a judicious mixture of both. Who wins critically depends on the common ratio used.

For a common ratio of zero (r=0), the candidate with the strongest support always wins; as only first preferences count. As the common ratio steadily increases, strong support becomes less important and broad support ever more important. Over the full range of r, the polarized candidate P drops from first to third place in the rankings.

For a common ratio approaching unity (r→1), the candidate with the broadest support always wins; refer to proof EM4. As the common ratio steadily decreases, broad support becomes less important and strong support ever more important. Over the full range of r, the consensus candidate C drops from first place to joint third in the rankings.

In between high and low common ratios, a candidate may win even if it is neither the one with the strongest or the broadest support; as highlighted in this example. Nevertheless, in order to simultaneously beat both a polarized candidate and a consensus one, a third candidate must have a powerful enough combination of strong and broad support. However, a candidate who has broader support as well as stronger support than any other candidate cannot be beaten.

In summary, polarized candidates are more likely to win when the common ratio is low. Conversely, consensus candidates are more likely to win when it is high. A non-extreme candidate but one with powerful support has its best chance of winning when the common ratio is intermediate in value such as with CHPV. For CHPV, as one first preference is worth the same as two second preferences, strong support and broad support are often equally valuable. When employing CHPV, candidates seeking election should campaign to both strengthen and broaden their appeal. Focusing on one type of support at the expense of the other risks losing the election.

Proceed to next section > Evaluations: Clones & Teaming

Return to previous page > Evaluations: Majority Criteria 3