Mathematical Proofs: Majority and Related Criteria
Proof EM4: Effect of Strong versus Broad Support as a function of Common Ratio
Scenario: Four candidates compete in a GV(r) election with fifteen voters. The polarized candidate P receives a minimal majority of first preferences from its eight supporters and last preferences from its seven opponents. The consensus candidate C is awarded a second preference by every voter. Of the two remaining challenger candidates, the leading one L receives all the remaining first preferences and a third preference from the other voters. The trailing challenger candidate T picks up the outstanding lower-value (third and fourth) preferences.
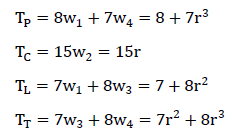
Using standard notation and formats, the profile for this GV(r) election scenario is given below.
- 8: P,C,L,T.
- 7: L,C,T,P.
Using the standard GV weightings (a,ar,ar2,ar3) where a = 1, the tally T for each candidate is derived and stated opposite.
To enable a graph of candidate tallies (T) against the full range of GV common ratios (0 ≤ r < 1) to be plotted (see main text), the table below provides the tally values for selected common ratios. As r=1 is invalid, r=0.99 is employed instead.
| Candidate Tallies (T) for selected common ratios (r) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Candidate | r=0 | r=0.1 | r=0.2 | r=0.3 | r=0.4 | r=0.5 | r=0.6 | r=0.7 | r=0.8 | r=0.9 | r=0.99 |
| P | 8 | 8.007 | 8.056 | 8.189 | 8.448 | 8.875 | 9.512 | 10.401 | 11.584 | 13.103 | 14.792 |
| C | 0 | 1.500 | 3.000 | 4.500 | 6.000 | 7.500 | 9.000 | 10.500 | 12.000 | 13.500 | 14.850 |
| L | 7 | 7.080 | 7.320 | 7.720 | 8.280 | 9.000 | 9.880 | 10.920 | 12.120 | 13.480 | 14.841 |
| T | 0 | 0.078 | 0.344 | 0.846 | 1.632 | 2.750 | 4.248 | 6.174 | 8.576 | 11.502 | 14.623 |
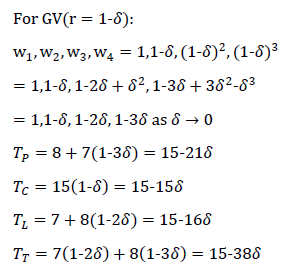
The four candidate tallies for a GV election where the common ratio r approaches unity is derived opposite.
For this special case, note that the weightings here form an arithmetic progression with δ as the common difference. Note too that rank positions also form an arithmetic progression but with a common difference of one. Hence, uplifting (or downgrading) a preference by one rank position raises (or lowers) its weighting by δ irrespective of the actual preference. Therefore, for any candidate, the higher its mean rank position is, the higher its tally is too as both changes are always directly proportional. Consequently, the candidate with the highest mean rank position is guaranteed to win any GV election when the common ratio approaches unity (r→1).
From the data opposite and in the above table, the collective rank order of the candidates for a GV election with an extreme or intermediate common ratio is shown below.
- P > L > C = T for GV(r=0)
- L > P > C > T for GV(r=1/2) = CHPV
- C > L > P > T for GV(r→1)
The polarized candidate P wins when a low common ratio is employed while the consensus candidate C is victorious when a high one is used instead. As this GV example demonstrates, where CHPV or an intermediate common ratio is employed, a leading challenger candidate L with a powerful combination of both strong and broad support may indeed be capable of simultaneously beating both a polarized candidate and a consensus one in a single-winner election.
Return to main text > Evaluations: Majority Criteria 4
Refer to > Mathematical Proofs: Table of Contents
