Evaluations: Teaming Thresholds 4

GV Teaming Thresholds as a function of the Common Ratio

On the preceding cloning maps for M = 1, 2, 3 & 4, twenty pairs of teaming thresholds are plotted. The same pairs are now redrawn on cloning maps for r = 0, 1/4, 1/2, 3/4 & 1. The teaming areas on all the following four maps are again highlighted in white but now for M = 1 only.

However, the r = 0 map is not shown here as the teaming thresholds for A₁ are all co-incident with the left-hand side of the map and those for A_K are all co-incident with the right-hand side. This (r = 0) cloning map is wholly grey regardless of the value of M. Therefore, except for ties, only vote splitting can occur.

First consider the consequences of teaming when the common ratio is less than one half but more than zero. The cloning map for r = 1/4 illustrates one such ratio. The white areas clearly shrink in size as M increases. Hence, for 0 < r < 1/2, a strategy that prevents teaming when M = 1 will be even more effective when M is larger.

The only viable anti-teaming strategy for non-A supporters is to reverse any slate issued by clone set A and therefore rank the fraternal clones in reverse order to that preferred by A supporters. If A does not issue a slate, then no reply should be required.

So if A supporters cast votes in proportion p = 1/2 (identical cloning) or p = 1 (fraternal cloning) where p = p_F or p_R, then how should non-A supporters react in terms of the proportion q where q = q_F or q_R? If p_F = p_R = 1/2 (central vertical challenge line), then no reaction to identical cloning is needed as any value of q results in vote splitting and A losing.

For fraternal cloning with p_R = 0 (left-hand vertical challenge line), reacting with q_F = 0 (bottom horizontal response line) maintains the original critical tie and thwarts teaming. For fraternal cloning with p_F = 0 (right-hand vertical challenge line), reacting with q_R = 0 (top horizontal response line) similarly maintains the original critical tie and thwarts teaming.

Where not all supporters are loyal to the issued slate direction, values of p_R or p_F will rise above zero towards one half. For these rising values of p, a widening range of q values exist to thwart teaming but the anti-teaming strategy of q = 0 remains the optimum response. Indeed, for p > r (provided that p < 1/2 and r < 1/2), then any value of q will ensure that A loses through vote splitting. Adopting the slate-reversal anti-teaming strategy always works for this range of r (0 < r < 1/2).

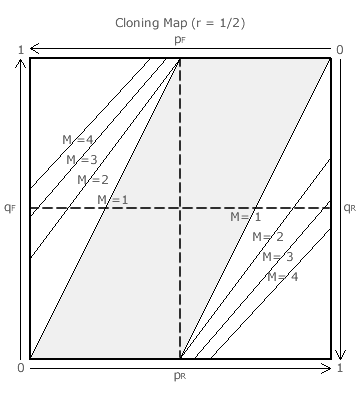
Next consider the very special case of CHPV. On the r = 1/2 cloning map, the M = 1 thresholds now end at the central vertical challenge line (where p_R = p_F = 1/2). Here, B will still win except only when either q_R or q_F = 0 where B and A₁ or B and A_K respectively remain tied.

However, as A has created identical clones by not issuing a slate, B has no slate to invert so q_F = q_R = 1/2 (central horizontal response line). Consequently, B does not need to reply and wins anyway through vote splitting.

In other respects, the performance of CHPV is similar to that of GV with a smaller value of r. Therefore, the anti-teaming strategy of slate-reversal works as well for CHPV as it does for lower common ratios.

Proceed to next page > Evaluations: Teaming Thresholds 5

Return to previous page > Evaluations: Teaming Thresholds 3