Evaluations: Teaming Thresholds 5
GV Teaming Thresholds as a function of the Common Ratio (continued)

Now consider the consequences of teaming when the common ratio is more than one half but less than one. The cloning map for r = 3/4 illustrates one such ratio. Two troubling features now appear on all such maps. Firstly, the horizontal width of each (white) teaming area now extends beyond one half of the map. For example, this width is 3/4 for M = 1 on the r = 3/4 map opposite.
Consequently, for some values of p centred around p = 1/2, replying with q = 0 actually backfires. For M = 1 on the r = 3/4 map, this central range of p is from 1/4 to 3/4. Although teaming is still thwarted for the intended clone (either A1 or AK), the other unintended one nevertheless snatches victory.
Secondly, as the gradient of each threshold line declines as M rises (for this range of r), the troublesome central range of p values actually increases as M rises. Further, as r increases, this same range of p values also widens. Often, this range extends from one side of the map to the other (0 ≤ p ≤ 1) as, for example, on the r = 3/4 map where M ≥ 3. Clearly, the anti-teaming retaliation strategy of slate-reversal fails to guarantee success for r > 1/2. Indeed, it becomes increasingly counterproductive as both r and M rise.
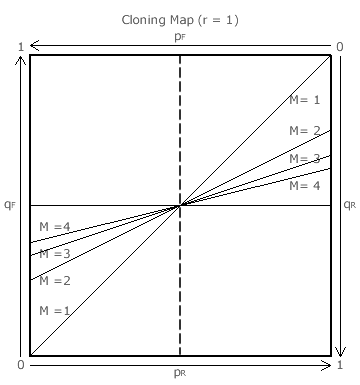
The teaming threshold equations are invalid for r = 1. Hence the cloning map for r = 1 opposite has been drawn for a value of r that is extremely close to 1 instead. Although the gradients of the threshold lines vary with M, they all pass through the centre of the map and each pair (those with the same M value) coincide so that the whole map is a (white) teaming area for any M. Except for ties, teaming always succeeds as for any p there is no q that counteracts it.
In conclusion, the anti-teaming strategy of slate-reversal is guaranteed to succeed for GV with common ratios no higher than one half. CHPV is therefore the upper limit for geometric voting where teaming is always capable of being thwarted. For GV with 0 < r ≤ 1/2, cloning is at best pointless for the prospective clone set but it otherwise inflicts self-harm; provided the slate-reversal anti-teaming strategy is adopted by its opponents. By using this strategy, other candidates do not then need to retaliate by cloning themselves.
GV Teaming Index
The size of the (white) teaming areas in the worst case (namely largest when M = 1) relative to the fixed size of the map provides a valuable indication of the extent to which GV is vulnerable to teaming for any given value of the common ratio r. This indicator or Teaming Index is easily deduced from the earlier cloning map for M = 1. For any r, both white areas are right-angled triangles of height 1 and width r. Therefore, as the area of each right-angled triangle is (height x width)/2, the combined teaming area is 2(1 x r)/2 or just r. As the area of the map is simply 1 x 1 = 1, then for a GV system with a common ratio of r, its Teaming Index is also equal to r.
Expressed as a percentage, the Teaming Index hence ranges linearly from 0% where only vote splitting occurs to 100% where only teaming happens. So, like the plurality (first-part-the-post) system, GV with r = 0 does not suffer from teaming. Also, like the Borda Count, GV with r → 1 does not experience vote splitting. Using this index, it is fair to say that CHPV is the GV variant mid-way between these two conflicting extremes.
Proceed to next page > Evaluations: Teaming Thresholds 6
Return to previous page > Evaluations: Teaming Thresholds 4
