Evaluations: Teaming Thresholds 2

GV Teaming Thresholds for Clone Set versus One Candidate

• q_F > p_R/r for A₁ to win through teaming.
• q_R > p_F/r for A_K to win through teaming.

In this first and simplest specific scenario, two candidates A and B are initially tied before clone set A nominates its K clones. As B is the only non-clone, M = 1. By comparing the tallies for A₁ and B and then A_K and B, the above two teaming threshold equations are determined.

To promote A₁ through teaming, a forward slate should be issued to maximise p_F. To thwart such an attempt, q_R should be maximised. To put it the other way round, p_R and q_F should both be minimised. Where q_F is larger than p_R/r, A₁ wins through teaming but, where q_F is smaller than p_R/r, B beats A₁ through vote splitting. A tie is maintained when the two expressions are equal.

For a challenge by A_K instead, p_F and q_R should now be minimised. Note that for B to win, B must simultaneously beat both A₁ and A_K.

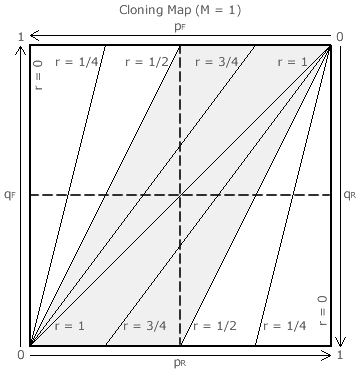
Each teaming threshold is equivalent to a straight line on the cloning map opposite; where M = 1. Example lines have been plotted for values of r ranging from 0 to 1 in steps of 1/4.

For any r, there are two areas where A wins through teaming and an intervening one where A loses to B through vote splitting. A₁ wins in the upper-left area and A_K in the lower-right one. For CHPV (r = 1/2) as an example, its two teaming areas are highlighted here in white and the intervening vote splitting area in grey.

GV Teaming Thresholds for Clone Set versus Two Candidates

• q_F > (1/2 + p_R/r)/(1+r) for A₁ to win through teaming.
• q_R > (1/2 + p_F/r)/(1+r) for A_K to win through teaming.

In this second specific scenario, three candidates A, B and C are initially all tied before clone set A nominates its K clones. As B and C are the only non-clones, M = 2. By comparing the tallies for A₁ and B (or C) and then A_K and B (or C), the above two teaming threshold equations are determined.

Example threshold lines are again drawn on the (M = 2) cloning map opposite for the same values of r as before. Also, for CHPV (r = 1/2) as an example, its upper-left white area (where A₁ wins), its lower-right white area (where A_K wins) and the intervening grey area (where B and C remain tied but beat both A₁ and A_K) are again shown.

For all points along a teaming threshold (boundary line between a white and grey area), a critical tie between the relevant leading A clone and all the M non-clone candidates is retained.

Proceed to next page > Evaluations: Teaming Thresholds 3

Return to previous page > Evaluations: Teaming Thresholds 1