Mathematical Proofs: Teaming Thresholds

Proof ET1: GV Teaming Thresholds for Clone Set versus One Candidate

Scenario: The election is conducted using GV and its standard weightings are used here to determine the tally (T) for any of the N candidates on the ballot. The weighting of the first preference is set at one (w₁ = a = 1) and the number of voters casting valid ballots is V. The clone set is A and it nominates K clones in total. On its forward slate, its clones are listed from A₁ to A_K. The reverse slate therefore lists these clones from A_K to A₁ in exactly the reverse sequence. In this first specific scenario, only one candidate B has been nominated to oppose the clone set A. All voters rank the clone candidates in either forward or reverse order.

• p_F = Of those preferring A first, the proportion who rank the clone set in forward slate order
• p_R = Of those preferring A first, the proportion who rank the clone set in reverse slate order
• q_F = Of those not preferring A first, the proportion who rank the clone set in forward slate order
• q_R = Of those not preferring A first, the proportion who rank the clone set in reverse slate order

Hence, for those preferring A first, p_F + p_R = 1 and, for those preferring B first, q_F + q_R = 1. Where all first preference A voters rank candidates in compliance with the forward slate, p_F = 1 and p_R = 0. Where they vote consistently for the reverse slate, p_R = 1 and p_F = 0. If no slate is issued and all clones are identical rather than fraternal, then p_F = 1/2 and p_R = 1/2. The same holds for first preference B voters except that the proportion p is now replaced by the proportion q.

For the clone set, there is no point in teaming if it would win anyway with just one candidate A. Therefore, its easiest opportunity to win unfairly through teaming is when it is tied with all the other competing candidates (just B here). This pre-cloning critical tie between both candidates is where each has one half of first preferences and one half of second preferences (T_A = T_B). After nominating its K clones, the profile for this election scenario is given below; using the standard notation and formats,

• p_FV/2: A₁,~~~,A_K,B.
• p_RV/2: A_K,~~~,A₁,B.
• q_FV/2: B,A₁,~~~,A_K.
• q_RV/2: B,A_K,~~~,A₁.

For clone A₁ to win through cloning, the tally for A₁ must exceed the one for B; namely T_A1 > T_B. To maximise the tally for A₁, clone set A should issue a forward slate to minimise the value of p_R. To minimise this same tally, B supporters should reverse the slate to minimise the value of q_F. By evaluating the tallies for A₁ and B, this key relationship between q_F and p_R - the teaming threshold for A₁ - can be derived as shown below.

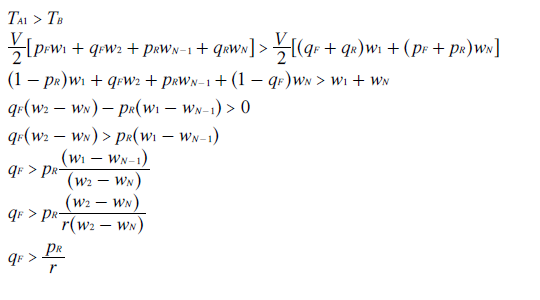
The above teaming threshold determines the relative ranking of A₁ and B as follows.

• For q_F > p_R/r, A₁ wins through successful teaming against B.
• For q_F = p_R/r, B and A₁ are still both tied.
• For q_F < p_R/r, B beats A₁ through vote splitting.

For clone A_K to win through cloning, the tally for A_K must exceed the one for B; namely T_AK > T_B. By evaluating the tallies for A_K and B, the key relationship between q_R and p_F - the teaming threshold for A_K - can be derived in exactly the same manner as above but with the _F and _R subscripts for p and q exchanged. This relationship is stated below.

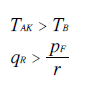
The above teaming threshold determines the relative ranking of A_K and B as follows.

• For q_R > p_F/r, A_K wins through successful teaming against B.
• For q_R = p_F/r, B and A_K are still both tied.
• For q_R < p_F/r, B beats A_K through vote splitting.

Note that to break the tie with A and win outright, B must simultaneously beat both A₁ and A_K.

Return to main text > Evaluations: Teaming Thresholds 2

Refer to > Mathematical Proofs: Table of Contents