Mathematical Proofs: Positional Voting

Proof CV4: Consensus Index Values for other Example Vectors

In the previous proof (CV2) the consensus and polarization indices for geometric voting are deduced. For comparison purposes, the same two bias indices for three other voting vectors are evaluated here. They are also derived in the same manner as before; see the Consensus and Polarization Indices for Geometric Voting proof.

The three selected example voting systems and the weighting function that defines each one are stated below.

• Nauru: w_n = 1/n
• Square: w_n = 1/n²
• Factorial: w_n = 1/n!

Nauru

The standard and normalized vectors for the voting system used in Nauru are stated below.

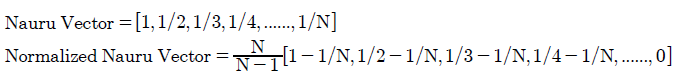
The sum of all the N preference weightings for the Nauru vector is derived below.

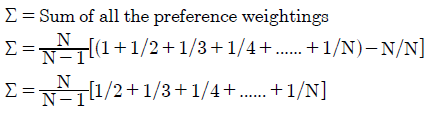
Using this sum Σ, the polarization and consensus indices are then easily calculated since PI_V = 1/Σ and CI_V = (Σ -1)/Σ. Notice that this sum and hence both bias indices vary with the number of candidates standing in an election.

Square

The standard and normalized vectors for the Square voting system are stated below.

The sum of all the N preference weightings for the Square vector is derived below.

Using this sum Σ, the polarization and consensus indices are then easily calculated since PI_V = 1/Σ and CI_V = (Σ -1)/Σ. Notice that this sum and hence both bias indices vary with the number of candidates standing in an election.

Factorial

The standard and normalized vectors for the Factorial voting system are stated below.

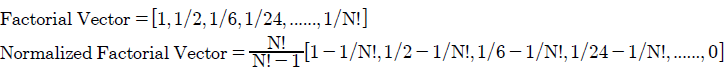
The sum of all the N preference weightings for the Factorial vector is derived below.

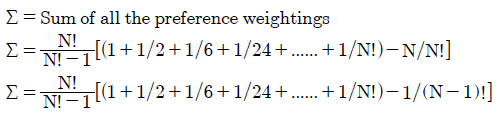
Using this sum Σ, the polarization and consensus indices are then easily calculated since PI_V = 1/Σ and CI_V = (Σ -1)/Σ. Notice that this sum and hence both bias indices vary with the number of candidates standing in an election.

Evaluation of the Consensus Index for each voting system with selected values of N

The first table below shows values of the sum Σ for each of the three example voting systems with up to ten candidates. The second table gives the corresponding Consensus Index (CI_V) value for each vector.

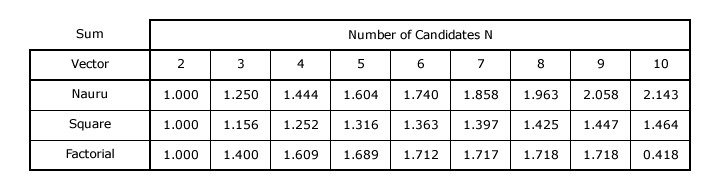
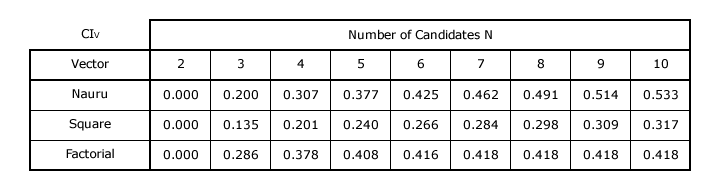
As the number of candidates increases, the consensus index for some vectors appears to converge on a particular value. The sum to infinity of all the preference weightings when the number of candidates is unlimited is finite for a convergent series of weightings but infinite for a divergent one. The following sums to infinity are provided in the Convergent Series section of the Wikipedia website. GV(r) is also included here for comparison. Note that a standard vector (where w₁ = 1) with an unlimited number of candidates (N →∞) is already normalized since its last weighting is zero (w_∞ = 0).

• Nauru with N = ∞: Σ = ∞ (Divergent series)
• Square with N = ∞: Σ = π²/6 (Convergent series)
• Factorial with N = ∞: Σ = e - 1 (Convergent series)
• GV(r) with N = ∞: Σ = 1/(1-r) (Convergent Series)

For the Nauru vector with an unlimited number of candidates, its sum Σ does not converge on any fixed value but tends to infinity. However, for the Square vector, its Σ does converge on a particular value as calculated below.

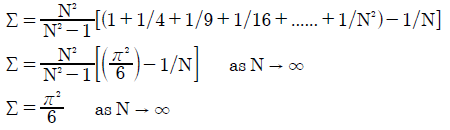
Similarly for the Factorial vector, its Σ too converges on a certain value as derived below.

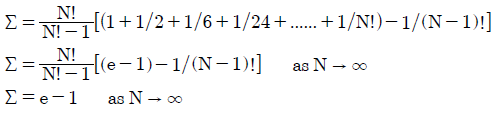
For an unlimited number of candidates, the consensus index for each of the selected vectors is calculated below.

• Nauru with N = ∞: CI_V = (Σ - 1)/Σ = (∞ - 1)/∞ = 1
• Square with N = ∞: CI_V = (Σ - 1)/Σ = (π²/6 - 1)/(π²/6) = 0.392
• Factorial with N = ∞: CI_V = (Σ - 1)/Σ = [(e - 1) - 1]/(e - 1) = 0.418
• GV(r) with N = ∞: CI_V = (Σ - 1)/Σ = [(1-r)^-1 - 1]/(1-r)^-1 = [1 - (1-r)]/1 = r

Notice that every bias index converges on a specific value as the number of candidates becomes ever larger. For any function with a divergent series of weights, Σ tends to infinity and so its consensus index converges on CI_V = 1. As N tends to infinity, PI_V and CI_V cease to be functions of N.

Return to main text > Comparisons: Positional Voting 6

Refer to > Mathematical Proofs: Table of Contents