Comparisons: Positional Voting 6

Bias Indices for other Example Voting Vectors

Although GV(r) can represent any positional voting system between Plurality and the Borda Count when only three candidates are nominated, it can only substitute for a few vectors when more candidates are fielded. Three alternative systems are investigated here in order to compare and contrast them to GV(r).

The voting system employed by the state of Nauru is an important positional voting one in its own right. The other two are called the 'Square' and 'Factorial' vectors due to their respective weightings formula. Neither is known to be used in practice but both are valid and illuminating methods. The standard formula for the nth weighting of the vector with N candidates and the standard vector itself for each of the three alternatives to GV(r) are given below.

• Nauru: w_n = 1/n for 1 ≤ n ≤ N
• Standard Nauru Vector = [1, 1/2, 1/3, 1/4, ......, 1/N]

• Square: w_n = 1/n² for 1 ≤ n ≤ N
• Standard Square Vector = [1, 1/4, 1/9, 1/16, ......, 1/N²]

• Factorial: w_n = 1/n! for 1 ≤ n ≤ N
• Standard Factorial Vector = [1, 1/2, 1/6, 1/24, ......, 1/N!]

The normalized vector and the equations for Σ, PI_V and CI_V are all determined in exactly the same manner as for GV(r) or any other vector. The resultant CI_V values for the three alternative systems are shown in the table below.

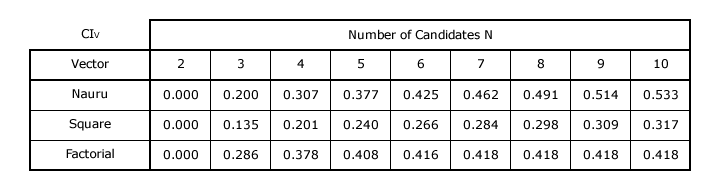
As with GV(r), when there are only two candidates the alternative vectors all produce the same wholly polarized election outcome. For all three vectors, their CI_V value rises as N increases and it does so more slowly as N becomes larger. The Factorial vector converges very rapidly towards its ultimate value. It is initially more consensual than the Nauru vector but this reverses when more than five candidates are nominated. The Nauru vector is however consistently more consensual than the Square one for any number of candidates.

Like GV(r) vectors, the equations for Σ, PI_V and CI_V when N becomes very large and tends to infinity are again greatly simplified here. The weightings used for Σ in the Nauru vector form a divergent series and so Σ itself tends to infinity. However, those for both the Square and Factorial vectors form a convergent series so a finite value for Σ emerges. The resultant values for Σ and CI_V for each alternative are provided below.

• Nauru with N→∞:       Σ → ∞       CI_V = 1
• Square with N→∞:     Σ = π²/6     CI_V = 0.392
• Factorial with N→∞:     Σ = e-1      CI_V = 0.418

Another example of an existing positional voting system is the one employed by the European Song Contest where many more than ten songs compete against each other. It does not employ a formula but its weighting vector is fully defined as 12, 10, 8, 7, 6, 5, 4, 3, 2, 1 and 0 for all the remaining songs. The sum of its normalized weights is 58/12 and so its CI_V = 46/58 = 0.793. It is therefore a largely consensual system.

Proceed to next page > Comparisons: Positional Voting 7

Return to previous page > Comparisons: Positional Voting 5