Comparisons: Positional Voting 7

Comparison of Bias in Positional Voting Systems

Having evaluated the various selected positional voting systems, they can now be compared against one another using their consensus indices. For GV(r), the values of r = 1/4 and r = 3/4 were selected as they are intermediate between Plurality and CHPV and between CHPV and the Borda Count respectively. Using the table data provided on the previous two pages, the figure below shows how the bias for each vector varies with the number of candidates standing.

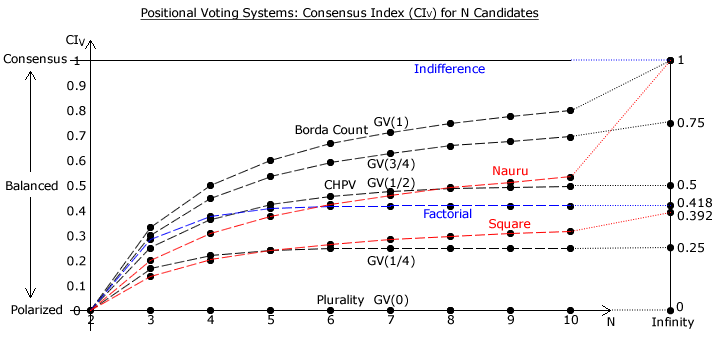
This plot shows a number of features that are independent of the number of candidates that are nominated. The Borda Count [≡ GV(r→1)] is consistently the most consensual of the valid vectors. Similarly, Plurality [≡ GV(r=0)] is always wholly polarized. As the common ratio r of a GV vector is increased, its CI_V is also increased.

As N increases, the CI_V of a GV(r) vector also increases but at an ever slower rate as N steadily rises. Where N becomes very large and tends to infinity, the index converges towards its asymptote of CI_V = r. The lower the value of r the more rapidly the bias approaches this asymptote.

The Borda Count and Nauru vectors both vary from CI_V = 0 at N = 2 to CI_V = 1 at N = ∞. However, the Nauru vector is consistently less consensual for other values of N. Both the Square and Factorial vectors are always partially biased towards polarization. However, the Factorial one is always less polarized than the Square one and its CI_V essentially converges onto its asymptote when relatively few candidates are fielded.

The weightings in any normalized vector must range from w₁ = 1 to w_N = 0 in N-1 steps. With few candidates, the average step size between adjacent weightings is relatively large and hence quite polarized even for otherwise consensual voting systems. With many candidates, the average step size is much smaller. In the Borda Count, every step size is the same as the average one. In any other vector some of the steps will necessarily be larger than the average and so it will be more polarized than the Borda Count. The selected positional voting systems are listed below in order of their bias from the most consensual to the most polarized when the number of candidates is quite large and ceases to influence this bias. The indifference vector (where w₁ = w_n = w_N = 1) is also listed for comparison but it is invalid since w₁ = w_N. Although the Borda Count is the most consensual valid vector, it never achieves perfect consensus unlike the pointless indifference vector.

• Indifference   (Invalid but CI_V = 1)
• Borda Count (Most consensual vector)
• Nauru
• GV(r=3/4)
• CHPV
• Factorial
• Square
• GV(r=1/4)
• Plurality     (Wholly polarized as PI_V = 1)

Proceed to next page > Comparisons: Positional Voting 8

Return to previous page > Comparisons: Positional Voting 6