Comparisons: Positional Voting 4

Three-Candidate GV(r) Conjugate Vectors and Anti-Vectors

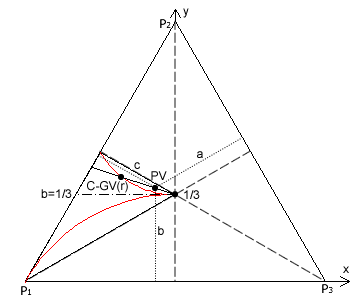
On page 2 of the Comparisons: Geometric Voting section, the location of three-preference GV(r) vectors is plotted on a triangular preference map. As the common ratio is varied over its entire range (0 ≤ r < 1), the trajectory of these vectors forms a circular arc from point P₁ to the map centre; as demonstrated in proof CG1. This arc is the lower red curve in the map opposite. The weightings of the preferences P₁, P₂ and P₃ are respectively w₁, w₂ and w₃. As the three map co-ordinates sum to unity, they are again a, b and c where a = w₁/W, b = w₂/W and c = w₃/W and W = w₁ + w₂ + w₃ for GV(r) vectors.

Conjugate vectors - unlike anti-vectors - may also be plotted on a three-preference map since they employ non-negative weightings. The weightings for any conjugate vector C-GV(r) are u₁ = 1 - w₃/W, u₂ = 1 - w₂/W and u₃ = 1 - w₁/W where W = w₁ + w₂ + w₃. The common ratio here for conjugate vectors is defined as r = w₂/w₁. As these conjugate weightings now sum to two, the corresponding preference map co-ordinates here are a = u₁/2 = (1 - w₃/W)/2, b = u₂/2, = (1 - w₂/W)/2 and c = u₃/2 = (1 - w₁/W)/2. The point C-GV(r) on the map opposite represents this conjugate vector.

All valid vectors and conjugate vectors lie within the white ranking region of the map. Recall that the horizontal line where b = 1/3 represents all the Borda Count equivalent positional voting systems; see Comparisons: Geometric Voting 1. All vectors are located on or below this line while all conjugate vectors are on or above it. All other locations on the map are invalid for positional voting.

• As the C-GV(r) common ratio is varied from r = 0 to r → 1, the trajectory of these conjugate vectors follows a circular arc from the mid-point of baseline P₁P₂ to the map centre; as shown by the upper red curve on the map above.

In proof CG2 it is demonstrated that all valid vectors along a straight line from the edge of the map to its centre are equivalent in terms of collective candidate rankings. The intersection of this line with the arc of GV(r) vectors identifies the equivalent GV(r) vector for these other vectors. Here, the value of the common ratio is derived as r = (b-c)/(a-b) = (w₂-w₃)/(w₁-w₂) in proof CG3. Similarly, a straight line through the arc of the conjugate vectors identifies an equivalent C-GV(r) to the others along this line; see the above map.

• For any valid positional voting conjugate vector (u₁,u₂,u₃), there exists an equivalent C-GV(r) and A-GV(r) vector where the value of its common ratio is r = (a-b)/(b-c) = (u₁-u₂)/(u₂-u₃).

Therefore, the following equivalences are established for all conjugate vectors and their corresponding anti-vectors.

Notice that the common ratio here is the difference between the first preference weighting and the second one divided by the difference between the second and third preference weightings. For ordinary vectors, the numerator and demoninator are transposed for this division.

For the Anti-Plurality conjugate vector (1,1,0), the equivalent A-GV(r) one is where r = (1-1)/(1-0) = 0. Hence, the mid-point along the baseline P₁P₂ where a = 1/2, b = 1/2 and c = 0 represents Anti-Plurality in both its C-GV(r=0) and A-GV(r=0) versions. In contrast, at the other extreme, apex P₁ represents both Plurality and GV(r=0). Note that the common ratio is zero for both extremes. The Anti-Borda-Count conjugate vector (1-0,1-1/3,1-2/3) equals (1,2/3,1/3) and this is equivalent to (2/3,1/3,0) for candidate rankings. Therefore, an Anti-Borda-Count conjugate vector is identical to the Borda Count vector. Hence, the horizontal line where b = 1/3 simultaneously represents GV(r → 1) vectors as well as both the C-GV(r → 1) and A-GV(r → 1) ones.

Bias indices for GV(r) conjugate vectors and anti-vectors are addressed in depth in Comparisons: Positional Voting 8.

Proceed to next page > Comparisons: Positional Voting 5

Return to previous page > Comparisons: Positional Voting 3