Comparisons: Positional Voting 5

Bias Indices for Geometric Voting

As GV(r=0) equates to Plurality and GV(r→1) to the Borda Count, evaluating the two bias indices for geometric voting for all valid values of r and N then enables all of the possible GV(r) vectors to be assessed simultaneously. The formula for the nth weighting of a GV(r) vector with N candidates, the standard vector itself and its normalized version are each given below.

• GV(r): w_n = r^n-1 for 1 ≤ n ≤ N
• Standard GV(r) Vector = [1, r, r², ......, r^N-2, r^N-1]
• Normalized GV(r) Vector = [1-r^N-1, r-r^N-1, r²-r^N-1, ......, r^N-2-r^N-1, 0]/(1-r^N-1)

The sum Σ of all the normalized preference weightings in the N-candidate GV(r) vector is stated below. The two bias indices PI_V and CI_V can then easily be calculated using this sum since PI_V = 1/Σ and CI_V = (Σ-1)/Σ.

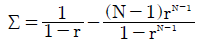
The sum and hence the two indices too are all functions of both the common ratio r and the number of candidates N. The table below shows values for the Consensus Index (CI_V) for selected values of the common ratio with up to ten candidates.

With only two candidates (N = 2), CI_V = 0 and PI_V = 1. Hence here, the GV(any r), Plurality and the Borda Count vectors are all wholly polarized and normalized to simply [1, 0]. All the differing voting systems generate the same election outcome in this special case. As required, GV(r=0) is consistently and extremely polarized regardless of N. For GV(r→1), with an increasing number of candidates this vector becomes ever more consensual. The Borda Count is not wholly consensual but it is always the most consensual vector regardless of N. This is clear from both the table above and the equation for Σ.

This raises the question of whether the CI_V index is meaningful if the Borda Count is not wholly consensual for any given election. So, consider the indifference vector where all its preference weightings are identical; namely w₁ = w_n = w_N. Since w₁ and w_N must have different values, this is actually an invalid voting vector and it cannot be normalized . However, as all its individual preference-pair CI_L indices are equal to one, the overall vector CI_V is also equal to one irrespective of N. Therefore, the invalid indifference vector - and not the Borda Count one - is the sole wholly-consensual vector. It is however pointless as it cannot discriminate between any of the candidates; hence its name.

Where the common ratio is between its two extreme values, the GV(r) vector also has an intermediate CI_V value that increases as r increases. As N increases for any given r, the CI_V value also rises but ever slower as the value of N becomes larger. Fortunately, as N becomes very large and tends towards infinity, the equation for the sum of all the weightings can be greatly simplified to Σ = 1/(1-r). The resultant simplified equations for the consensus and polarization indices are shown below.

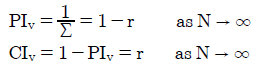
As N tends to infinity, the two bias indices cease to be functions of N and the CI_V converges on a unique value that is equal to the common ratio of the vector. Here the Borda Count vector does indeed approach a CI_V of 1 and CHPV (GV with r = 1/2) approaches a CI_V and PI_V of 1/2. Hence, for every extra candidate that enters the election, CHPV converges asymptotically towards being balanced exactly midway between Plurality and the Borda Count where there is no bias towards either extreme.

Proceed to next page > Comparisons: Positional Voting 6

Return to previous page > Comparisons: Positional Voting 4