Comparisons: Positional Voting 9

Effect of Truncation on GV(r) Bias Indices

The inherent system bias in a vector must not be confused with voter bias as expressed by preferred candidate rankings. Both candidates and vectors may be described as polarized or consensual but they are distinctly different features of an election. No matter how voters actually cast their individual preferences, the bias indices for the election vector are independent and fixed. There is however one caveat to this statement. When vector truncation occurs as part of the election method, this does alter the bias indices to some degree. Otherwise, these system indices are never affected by any individual voter preferences or truncation of them.

To illustrate the effect of truncation on a vector, consider a four-candidate GV(r) election example using CHPV. The standard vector and its normalized equivalent one (U) is shown in the first line below. The truncated vector (T) where the last preference weighting is set to zero is shown in the second line. The sum Σ, the PI and the CI for each vector are also included here.

• U vector: [1, 1/2, 1/4, 1/8] ≡ [1, 3/7, 1/7, 0], Σ_U = 11/7, PI_U = 7/11, CI_U = 4/11 = 0.3636
• T vector: [1, 1/2, 1/4, 0], Σ_T = 7/4, PI_T = 4/7, CI_T = 3/7 = 0.4286

In this example, vector truncation has resulted in less polarization and so greater consensus.

In fact, this shift towards consensus and away from polarization always occurs regardless of the vector selected; provided r ≠ 0 and N > 2. For r = 0 and for N = 2 the vector remains wholly polarized. Only the magnitude of the shift is specific to the actual vector. The relationships shown opposite hence apply to all vectors with three or more candidates; except Plurality. For GV(r), truncation of the last preference always promotes increased consensus.

Continuing with the four-candidate CHPV election vector example, the effect of truncation on a close contest between two polarized candidates (A and B) and one of two consensus candidates (C and D) can be demonstrated. Each polarized candidate is awarded a first preference by half of the voters and a fourth preference by the other half. The leading consensus candidate C receives a second preference from all the voters and the other one D hence gets a third preference from all voters. The resultant tallies for each candidate before and after truncation of the fourth and lowest rank preference are shown below.

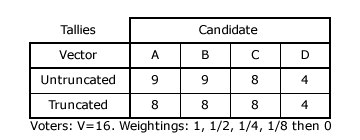
Before truncation, its CI_U = 0.3636 so the vector is somewhat polarized compared to a balanced one with no bias in either direction (CI = PI = 0.5). Here, the two starkly polarized candidates tie with each other but jointly beat both the wholly consensus candidates. Note that the voting system is only mildly polarized while the candidates are all heavily biased toward one extreme or the other. System bias and voter bias towards candidates are distinctly separate properties.

After truncation, its CI_T = 0.4286 so the vector is now still partially polarized but less so than before. Notice that the shift towards increased consensus resulting from truncation has awarded the leading consensus candidate C an increased share of the vote and so now a two-way tie between A and B has been converted into a three-way one between A, B and C. The truncation of the lowest preference from 1/8 to 0 has effectively raised the weighting of each other rank relative to the rank above in adjacent pairs; hence boosting consensus.

In this election example, only the last preference of the CHPV vector was truncated. Truncating further rank positions will reverse the direction of bias such that the vector then gradually becomes more polarized. Again continuing with the same election example, the sum Σ, the PI and the CI for the vector are as stated below when further weightings are truncated.

• T vector with 2 truncations: [1, 1/2, 0, 0], Σ_T2 = 3/2, PI_T2 = 2/3, CI_T2 = 1/3 = 0.3333
• T vector with 3 truncations: [1, 0, 0, 0], Σ_T3 = 1, PI_T3 = 1, CI_T3 = 0

Notice that as a result of the first truncation (of the last preference), the vector is automatically normalized and that any further truncations do not require any re-normalization of the new vector. Therefore, any truncated intermediate weighting is simply removed with no rescaling of any higher intermediate ones required. Consequently, the sum Σ decreases with each removed weighting and so greater polarization is witnessed. When only the first preference is left untruncated, the vector becomes wholly polarized and equivalent to Plurality.

Proceed to next page > Comparisons: Positional Voting 10

Return to previous page > Comparisons: Positional Voting 8